题目内容
7.已知函数f(x)=Asin(2x+φ)-$\frac{1}{2}$(A>0,0<φ<$\frac{π}{2}$)的图象在y轴上的截距为1,且关于直线x=$\frac{π}{12}$对称,若对于任意的x∈[0,$\frac{π}{2}$],都有m2-3m≤f(x),则实数m的取值范围为( )| A. | [1,$\frac{3}{2}$] | B. | [1,2] | C. | [$\frac{3}{2}$,2] | D. | [$\frac{3-\sqrt{3}}{2}$,$\frac{3+\sqrt{3}}{2}$] |
分析 利用函数y=Asin(ωx+φ)+B的图象和性质,正弦函数的定义域和值域,求得实数m的取值范围.
解答 解:∵函数f(x)=Asin(2x+φ)-$\frac{1}{2}$(A>0,0<φ<$\frac{π}{2}$)的图象在y轴上的截距为1,
∴Asinφ-$\frac{1}{2}$=1,即Asinφ=$\frac{3}{2}$.
∵函数f(x)=Asin(2x+φ)-$\frac{1}{2}$ 的图象关于直线x=$\frac{π}{12}$对称,∴2•$\frac{π}{12}$+φ=kπ+$\frac{π}{2}$,k∈Z,∴φ=$\frac{π}{3}$,
∴A•sin$\frac{π}{3}$=$\frac{3}{2}$,∴A=$\sqrt{3}$,∴f(x)=$\sqrt{3}$sin(2x+$\frac{π}{3}$)-$\frac{1}{2}$.
对于任意的x∈[0,$\frac{π}{2}$],都有m2-3m≤f(x),
∵2x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{4π}{3}$],sin(2x+$\frac{π}{6}$)∈[-$\frac{\sqrt{3}}{2}$,1],$\sqrt{3}$sin(2x+$\frac{π}{6}$)∈[-$\frac{3}{2}$,$\sqrt{3}$],f(x)∈[-2,$\sqrt{3}$-1],
∴m2-3m≤-2,求得1≤m≤2,
故选:B.
点评 本题主要考查函数y=Asin(ωx+φ)+B的图象和性质,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
13.设l,m,n表示三条直线,α,β,γ表示三个平面,则下面命题中不成立的是( )
| A. | 若l⊥α.m⊥α,则l∥m | |
| B. | 若m?β,m⊥l,n是l在β内的射影,则m⊥n | |
| C. | 若m?α,n?α,m∥n,则n∥α | |
| D. | 若α⊥γ,β⊥γ,则α∥β. |
15.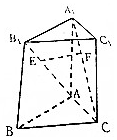 如图,在三棱柱ABC-A1B1C1中,已知E,F分别是线段AB1与CA1上的动点,异面直线AB1与CA1所成角为θ,记线段EF中点M的轨边为L,则|L|等于( )
如图,在三棱柱ABC-A1B1C1中,已知E,F分别是线段AB1与CA1上的动点,异面直线AB1与CA1所成角为θ,记线段EF中点M的轨边为L,则|L|等于( )
 如图,在三棱柱ABC-A1B1C1中,已知E,F分别是线段AB1与CA1上的动点,异面直线AB1与CA1所成角为θ,记线段EF中点M的轨边为L,则|L|等于( )
如图,在三棱柱ABC-A1B1C1中,已知E,F分别是线段AB1与CA1上的动点,异面直线AB1与CA1所成角为θ,记线段EF中点M的轨边为L,则|L|等于( )| A. | $\frac{1}{2}$|AB1| | |
| B. | $\sqrt{{\overrightarrow{A{B}_{1}}}^{2}+{\overrightarrow{C{A}_{1}}}^{2}-(\overrightarrow{A{B}_{1}}•\overrightarrow{C{A}_{1}})^{2}}$ | |
| C. | $\frac{1}{4}$|AB1|•|CA1|•sinθ | |
| D. | $\frac{1}{12}$•V${\;}_{{\;}_{ABC-{A}_{1}{B}_{1}{C}_{1}}}$(V${\;}_{ABC-{A}_{1}{B}_{1}{C}_{1}}$是三棱柱ABC-A1B1C1的体积) |
19.椭圆E的焦点在x轴上,中心在原点,其短轴上的两个顶点和两个焦点恰为边长是2的正方形的顶点,则椭圆E的标准方程为( )
| A. | $\frac{x^2}{2}+\frac{y^2}{{\sqrt{2}}}=1$ | B. | $\frac{x^2}{2}+{y^2}=1$ | C. | $\frac{x^2}{4}+\frac{y^2}{2}=1$ | D. | $\frac{y^2}{4}+\frac{x^2}{2}=1$ |
17.设全集U={-2,-1,0,1,2},A={x|x≤1},B={-2,0,2},则∁U(A∩B)=( )
| A. | {-2,0} | B. | {-2,0,2} | C. | {-1,1,2} | D. | {-1,0,2} |
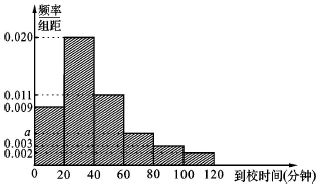 某校收集该校学生从家到学校的时间后,制作成如下的频率分布直方图:
某校收集该校学生从家到学校的时间后,制作成如下的频率分布直方图: