题目内容
9.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的两个焦点为F1、F2,点A在双曲线第一象限的图象上,若△AF1F2的面积为1,且tan∠AF1F2=$\frac{1}{2}$,tan∠AF2F1=-2,则双曲线方程为$\frac{{12{x^2}}}{5}-3{y^2}=1$.分析 设A(m,n).m>0,n>0.由tan∠AF1F2可得$\frac{n}{m+c}$=$\frac{1}{2}$,由tan∠AF2F1=-2可得$\frac{n}{m-c}$=2,由△AF1F2的面积为1可得$\frac{1}{2}$•2c•n=1,联立求出A的坐标,即可得出双曲线的方程.
解答 解:设A(m,n).m>0,n>0.
由tan∠AF1F2可得$\frac{n}{m+c}$=$\frac{1}{2}$,
由tan∠AF2F1=-2可得$\frac{n}{m-c}$=2,
由△AF1F2的面积为1可得$\frac{1}{2}$•2c•n=1,
以上三式联立解得:c=$\frac{\sqrt{3}}{2}$,m=$\frac{5\sqrt{3}}{6}$,n=$\frac{2\sqrt{3}}{3}$.
所以A($\frac{5\sqrt{3}}{6}$,$\frac{2\sqrt{3}}{3}$),F1(-$\frac{\sqrt{3}}{2}$,0),F2($\frac{\sqrt{3}}{2}$,0).
根据双曲线定义可得2a=|AF1|-|AF2|=$\frac{\sqrt{15}}{3}$.
所以a=$\frac{\sqrt{15}}{6}$,b=$\frac{1}{3}$,
所以双曲线方程为$\frac{{12{x^2}}}{5}-3{y^2}=1$.
故答案为$\frac{{12{x^2}}}{5}-3{y^2}=1$.
点评 本题主要考查了双曲线的简单性质.考查了学生对双曲线基础知识的理解和灵活利用.

练习册系列答案
相关题目
17.为了得到函数y=sin(2x-$\frac{π}{3}$)的图象,只需将函数y=sin2x的图象上所有的点( )
| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向左平移$\frac{π}{3}$个单位 | ||
| C. | 向右平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |
14.已知f(x)=x2+2xf′(-1),则f′(0)等于( )
| A. | 4 | B. | 0 | C. | -2 | D. | 2 |
1.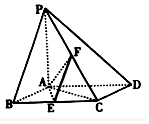 如图,已知四棱锥P-ABCD,地面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,地面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
(1)证明:AE⊥PD;
(Ⅱ)若AB=2,PA=2,求四面体P-AEF的体积.
 如图,已知四棱锥P-ABCD,地面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,地面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.(1)证明:AE⊥PD;
(Ⅱ)若AB=2,PA=2,求四面体P-AEF的体积.
18.已知三棱锥P-ABC的四个顶点P,A,B,C都在半径为R的同一个球面上,若PA,PB,PC两两相互垂直,且PA=1,PB=2,PC=3,则R等于( )
| A. | $\frac{{\sqrt{14}}}{2}$ | B. | $\sqrt{14}$ | C. | $\frac{{\sqrt{13}}}{2}$ | D. | $\sqrt{3}$ |