题目内容
在直角坐标系xOy中,已知点A(1,1),B(2,3),C(3,2),点P(x,y)在△ABC三边围成的区域(含边界)上,且
=m
+n
(m,n∈R)
(Ⅰ)若m=n=
,求|
|;
(Ⅱ)用x,y表示m-n,并求m-n的最大值.
| OP |
| AB |
| AC |
(Ⅰ)若m=n=
| 2 |
| 3 |
| OP |
(Ⅱ)用x,y表示m-n,并求m-n的最大值.
考点:简单线性规划
专题:数形结合,平面向量及应用
分析:(Ⅰ)由点的坐标求出向量
和
的坐标,结合m=n=
,再由
=m
+n
求得
的坐标,然后由模的公式求模;
(Ⅱ)由
=m
+n
得到
,作差后得到m-n=y-x,令y-x=t,然后利用线性规划知识求得m-n的最大值.
| AB |
| AC |
| 2 |
| 3 |
| OP |
| AB |
| AC |
| OP |
(Ⅱ)由
| OP |
| AB |
| AC |
|
解答:
解:(Ⅰ)∵A(1,1),B(2,3),C(3,2),
∴
=(1,2),
=(2,1),
又m=n=
,
∴
=
(1,2)+
(2,1)=(2,2).
∴|
|=
=2
;
(Ⅱ)∵
=m(1,2)+n(2,1)=(m+2n,2m+n),
∴
,两式相减得,m-n=y-x.
令y-x=t,由图可知,

当直线y=x+t过点B(2,3)时,t取得最大值1,
故m-n的最大值为:1.
∴
| AB |
| AC |
又m=n=
| 2 |
| 3 |
∴
| OP |
| 2 |
| 3 |
| 2 |
| 3 |
∴|
| OP |
| 22+22 |
| 2 |
(Ⅱ)∵
| OP |
∴
|
令y-x=t,由图可知,

当直线y=x+t过点B(2,3)时,t取得最大值1,
故m-n的最大值为:1.
点评:本题考查了平面向量的数乘及坐标加法运算,考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
若复数z=
,其中i为虚数单位,则z的虚部为( )
| 1+i |
| i |
| A、-1 | B、1 | C、i | D、-i |
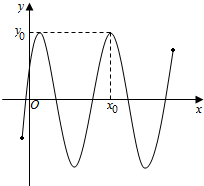 函数f(x)=3sin(2x+
函数f(x)=3sin(2x+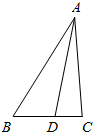 如图,在△ABC中,∠B=
如图,在△ABC中,∠B=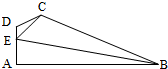 如图,在平面四边形ABCD中,DA⊥AB,DE=1,EC=
如图,在平面四边形ABCD中,DA⊥AB,DE=1,EC=