题目内容
若等差数列{an}满足a7+a8+a9>0,a7+a10<0,则当n= 时,{an}的前n项和最大.
考点:等差数列的性质
专题:等差数列与等比数列
分析:可得等差数列{an}的前8项为正数,从第9项开始为负数,进而可得结论.
解答:
解:由等差数列的性质可得a7+a8+a9=3a8>0,
∴a8>0,又a7+a10=a8+a9<0,∴a9<0,
∴等差数列{an}的前8项为正数,从第9项开始为负数,
∴等差数列{an}的前8项和最大,
故答案为:8.
∴a8>0,又a7+a10=a8+a9<0,∴a9<0,
∴等差数列{an}的前8项为正数,从第9项开始为负数,
∴等差数列{an}的前8项和最大,
故答案为:8.
点评:本题考查等差数列的性质和单调性,属中档题.

练习册系列答案
相关题目
在“世界读书日”前夕,为了了解某地5000名居民某天的阅读时间,从中抽取了200名居民的阅读时间进行统计分析,在这个问题中,5000名居民的阅读时间的全体是( )
| A、总体 |
| B、个体 |
| C、样本的容量 |
| D、从总体中抽取的一个样本 |
某次联欢会要安排三个歌舞类节目,2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是( )
| A、72 | B、120 |
| C、144 | D、168 |
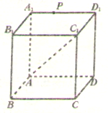 如图,P是正方体ABCD-A1B1C1D1上一动点,设点P和直线AC1确定的平面为α,过点P与直线AC1垂直的平面为β,则下列命题正确的序号是
如图,P是正方体ABCD-A1B1C1D1上一动点,设点P和直线AC1确定的平面为α,过点P与直线AC1垂直的平面为β,则下列命题正确的序号是