题目内容
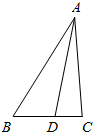如图，在△ABC中，∠B=| π |
| 3 |
| 1 |
| 7 |
（1）求sin∠BAD；
（2）求BD，AC的长．
考点：余弦定理的应用
专题：解三角形
分析：根据三角形边角之间的关系，结合正弦定理和余弦定理即可得到结论．
解答：
解：（1）在△ABC中，∵cos∠ADC=
，
∴sin∠ADC=
=
=
=
，
则sin∠BAD=sin（∠ADC-∠B）=sin∠ADC•cosB-cos∠ADC•sinB=
×
-
×
=
．
（2）在△ABD中，由正弦定理得BD=
=
=3，
在△ABC中，由余弦定理得AC2=AB2+CB2-2AB•BCcosB=82+52-2×8×5×
=49，
即AC=7．
| 1 |
| 7 |
∴sin∠ADC=
| 1-cos2∠ADC |
1-(
|
|
4
| ||
| 7 |
则sin∠BAD=sin（∠ADC-∠B）=sin∠ADC•cosB-cos∠ADC•sinB=
4
| ||
| 7 |
| 1 |
| 2 |
| 1 |
| 7 |
| ||
| 2 |
3
| ||
| 14 |
（2）在△ABD中，由正弦定理得BD=
| AB•sin∠BAD |
| sin∠ADB |
8×
| ||||
|
在△ABC中，由余弦定理得AC2=AB2+CB2-2AB•BCcosB=82+52-2×8×5×
| 1 |
| 2 |
即AC=7．
点评：本题主要考查解三角形的应用，根据正弦定理和余弦定理是解决本题本题的关键，难度不大．
练习册系列答案
相关题目
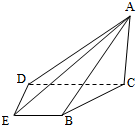如图，在四棱锥A-BCDE中，平面ABC⊥平面BCDE，∠CDE=∠BED=90°，AB=CD=2，DE=BE=1，AC=