题目内容
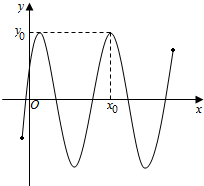 函数f(x)=3sin(2x+
函数f(x)=3sin(2x+| π |
| 6 |
(Ⅰ)写出f(x)的最小正周期及图中x0,y0的值;
(Ⅱ)求f(x)在区间[-
| π |
| 2 |
| π |
| 12 |
考点:三角函数的周期性及其求法,正弦函数的定义域和值域
专题:三角函数的图像与性质
分析:(Ⅰ)由题目所给的解析式和图象可得所求;(Ⅱ)由x∈[-
,-
]可得2x+
∈[-
,0],由三角函数的性质可得最值.
| π |
| 2 |
| π |
| 12 |
| π |
| 6 |
| 5π |
| 6 |
解答:
解:(Ⅰ)∵f(x)=3sin(2x+
),
∴f(x)的最小正周期T=
=π,
可知y0为函数的最大值3,x0=
;
(Ⅱ)∵x∈[-
,-
],
∴2x+
∈[-
,0],
∴当2x+
=0,即x=-
时,f(x)取最大值0,
当2x+
=-
,即x=-
时,f(x)取最小值-3
| π |
| 6 |
∴f(x)的最小正周期T=
| 2π |
| 2 |
可知y0为函数的最大值3,x0=
| 7π |
| 6 |
(Ⅱ)∵x∈[-
| π |
| 2 |
| π |
| 12 |
∴2x+
| π |
| 6 |
| 5π |
| 6 |
∴当2x+
| π |
| 6 |
| π |
| 12 |
当2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
点评:本题考查三角函数的图象和性质,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
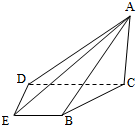 如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=
如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC= 如图,已知两条抛物线E1:y2=2p1x(p1>0)和E2:y2=2p2x(p2>0),过原点O的两条直线l1和l2,l1与E1,E2分别交于A1、A2两点,l2与E1、E2分别交于B1、B2两点.
如图,已知两条抛物线E1:y2=2p1x(p1>0)和E2:y2=2p2x(p2>0),过原点O的两条直线l1和l2,l1与E1,E2分别交于A1、A2两点,l2与E1、E2分别交于B1、B2两点.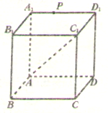 如图,P是正方体ABCD-A1B1C1D1上一动点,设点P和直线AC1确定的平面为α,过点P与直线AC1垂直的平面为β,则下列命题正确的序号是
如图,P是正方体ABCD-A1B1C1D1上一动点,设点P和直线AC1确定的平面为α,过点P与直线AC1垂直的平面为β,则下列命题正确的序号是