题目内容
设数列{an}中,a1=1,an+1=
(n∈N*),若am=
,则m= .
| an |
| an+1 |
| 1 |
| 5 |
考点:数列递推式
专题:等差数列与等比数列
分析:根据条件取倒数,根据等差数列数列的定义构造数列{
},即可得到结论.
| 1 |
| an |
解答:
解:∵a1=1,an+1=
,
∴取倒数得
=
=1+
,
则{
}是公差d=1的等差数列,首项为1,
则
=1+(n-1)=n,
则an=
,若am=
,即
=
,
解得m=5,
故答案为:5
| an |
| an+1 |
∴取倒数得
| 1 |
| an+1 |
| an+1 |
| an |
| 1 |
| an |
则{
| 1 |
| an |
则
| 1 |
| an |
则an=
| 1 |
| n |
| 1 |
| 5 |
| 1 |
| m |
| 1 |
| 5 |
解得m=5,
故答案为:5
点评:本题主要考查数列项的计算,根据条件构造数列{
}为等差数列是解决本题的关键.
| 1 |
| an |

练习册系列答案
相关题目
已知f(x)是定义在R上的奇函数,且x≥0时f(x)的图象如图所示,则f(-2)=( )
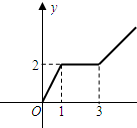
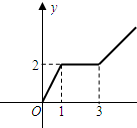
| A、-3 | B、-2 | C、-1 | D、2 |