题目内容
4.下列各组函数中表示同一个函数的是④①f(x)=x2与g(x)=(x+1)2;
②f(x)=(x一1)0与g(x)=1;
③f(x)=x-1与g(x)=$\sqrt{(x-1)^{2}}$;
④f(x)=|x|与g(t)=$\sqrt{{t}^{2}}$;
⑤f(x)=$\frac{(x-1)•\sqrt{x-2}}{x-1}$,g(x)=$\sqrt{x-2}$;
⑥f(x)=$\frac{{x}^{2}-1}{x-1}$与g(x)=x+1.
分析 同一函数是指函数的定义域、值域、对应关系均相同的函数,从这三要素入手,即可做出准确判断
解答 解:①f(x)=x2与g(x)=(x+1)2,对应法则不同,故不是,
②f(x)=(x一1)0的定义域为x≠1,g(x)=1的定义域为R,故不是,
③f(x)=x-1的值域为R,g(x)=$\sqrt{(x-1)^{2}}$的值域为[0,+∞),即对应法则不同,故不是,
④f(x)=|x|与g(t)=$\sqrt{{t}^{2}}$,定义域、值域、对应关系均相同,故是,
⑤f(x)=$\frac{(x-1)•\sqrt{x-2}}{x-1}$与g(x)=$\sqrt{x-2}$的定义域不同,故不是,
⑥f(x)=$\frac{{x}^{2}-1}{x-1}$与g(x)=x+1的定义域不同,故不是,
故答案为:④.
点评 本题考查了函数的定义及函数的三要素,属概念辨析题,较容易

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
14.已知随机变量ξ~N(3,a2),且cosφ=P(ξ>3)(其中φ为锐角),若函数f(x)=2sin(ωx+φ)(ω>0)的图象与直线y=2相邻的两交点之间的距离为π,则函数f(x)的一条对称轴为( )
| A. | x=$\frac{π}{12}$ | B. | x=$\frac{π}{6}$ | C. | x=$\frac{π}{3}$ | D. | x=$\frac{π}{2}$ |
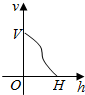
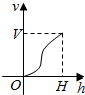
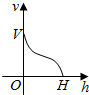
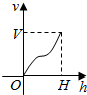
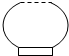 一高为H,满缸水量为V的鱼缸截面如图所示,其底部破了一个小洞,缸中水从洞中流出,若鱼缸水深为h时水的体积为v,则函数v=f(h)的大致图象可能是图中四个选项中的( )
一高为H,满缸水量为V的鱼缸截面如图所示,其底部破了一个小洞,缸中水从洞中流出,若鱼缸水深为h时水的体积为v,则函数v=f(h)的大致图象可能是图中四个选项中的( )