题目内容
14.已知随机变量ξ~N(3,a2),且cosφ=P(ξ>3)(其中φ为锐角),若函数f(x)=2sin(ωx+φ)(ω>0)的图象与直线y=2相邻的两交点之间的距离为π,则函数f(x)的一条对称轴为( )| A. | x=$\frac{π}{12}$ | B. | x=$\frac{π}{6}$ | C. | x=$\frac{π}{3}$ | D. | x=$\frac{π}{2}$ |
分析 由题意,随机变量ξ~N(3,a2),且cosφ=P(ξ>3)(其中φ为锐角),可得φ=$\frac{π}{3}$,T=π=$\frac{2π}{ω}$,可得ω=2,即可求出函数f(x)=2sin(2x+$\frac{π}{3}$)的一条对称轴.
解答 解:由题意,随机变量ξ~N(3,a2),且cosφ=P(ξ>3)(其中φ为锐角),
∴φ=$\frac{π}{3}$
T=π=$\frac{2π}{ω}$,∴ω=2,
∴函数f(x)=2sin(2x+$\frac{π}{3}$)的一条对称轴为x=$\frac{π}{12}$.
故选:A.
点评 本题考查正态分布图象的对称性,考查三角函数的性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
5.已知向量$\overrightarrow{m}$=(sinA,$\frac{1}{2}$)与向量$\overrightarrow{n}$=(3,sinA+$\sqrt{3}$cosA)共线,其中A是△ABC的内角,则角A的大小为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
2.我国古代数学名著《续古摘奇算法》(杨辉)一书中有关于三阶幻方的问题:将1,2,3,4,5,6,7,8,9分别填入3×3的方格中,使得每一行,每一列及对角线上的三个数的和都相等(如图所示),我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
| 8 | 3 | 4 |
| 1 | 5 | 9 |
| 6 | 7 | 2 |
| A. | 9 | B. | 8 | C. | 6 | D. | 4 |
9.已知实数a、b满足(a+i)(1-i)=3+bi,则复数a+bi的模为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 5 |
6.已知A(-1,0),B(2,0),平面内与点A距离为1,且与点B距离为2的直线的条数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
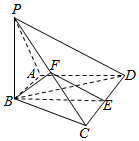 如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是棱CD和PC的中点.
如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是棱CD和PC的中点.