题目内容
16．
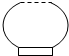一高为H，满缸水量为V的鱼缸截面如图所示，其底部破了一个小洞，缸中水从洞中流出，若鱼缸水深为h时水的体积为v，则函数v=f（h）的大致图象可能是图中四个选项中的（ ）| A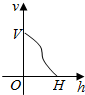． |  | B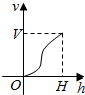． |  | C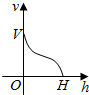． |  | D． |  |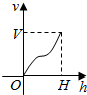
分析 水深h越大，水的体积v就越大，故函数v=f（h）是个增函数，一开始增长越来越快，后来增长越来越慢，图象是先凹后凸的．
解答 解：由图得水深h越大，水的体积v就越大，故函数v=f（h）是个增函数． 据四个选项提供的信息，
当h∈[O，H]，我们可将水“流出”设想成“流入”，
这样每当h增加一个单位增量△h时，
根据鱼缸形状可知，函数V的变化，开始其增量越来越大，但经过中截面后则增量越来越小，
故V关于h的函数图象是先凹后凸的，曲线上的点的切线斜率先是逐渐变大，后又逐渐变小，
故选：B．
点评 本题考查了函数图象的变化特征，函数的单调性的实际应用，体现了数形结合的数学思想和逆向思维，属于中档题．
练习册系列答案
相关题目
7．下列函数是奇函数的是（ ）
| A． | f（x）=x4 | B． | f（x）=x+$\frac{1}{x}$ | C． | f（x）=x3-1 | D． | f（x）=$\frac{1}{{x}^{2}}$ |
11．若集合A={x|3+2x-x2＞0}，集合B={x|2x＜2}，则A∩B等于（ ）
| A． | （1，3） | B． | （-∞，-1） | C． | （-1，1） | D． | （-3，1） |
8．已知函数f（x）=$\left\{\begin{array}{l}{2{e}^{-x-1}，x＜-1}\\{（2a-1）x-2a，x≥-1}\end{array}\right.$若函数f（x）的值域为R，则实数a的取值范围为（ ）
| A． | a≤-$\frac{1}{4}$ | B． | a＜$\frac{1}{2}$ | C． | -$\frac{1}{4}$≤a＜$\frac{1}{2}$ | D． | a＞$\frac{1}{2}$ |
6．将函数$y=sin（2x+\frac{π}{3}）$的图象向右平移$\frac{π}{4}$个单位，再向上平移1个单位，所得函数图象对应的解析式为（ ）
| A． | $y=sin（2x+\frac{π}{12}）+1$ | B． | $y=sin（2x-\frac{π}{12}）+1$ | C． | $y=sin（2x-\frac{π}{6}）+1$ | D． | $y=sin（2x+\frac{π}{6}）+1$ |