题目内容
15.已知条件p:A={x∈R|x2+ax+1=0},q:B={x∈R|x2-3x+2≤0},若p是q的充分条件,求实数a的取值范围.分析 由p是q的充分不必要条件,条件p:A={x∈R|x2+ax+1=0},q:B={x∈R|x2-3x+2≤0}={x|1≤x≤2},得到p⇒q,q不能推出p,即A是B的真子集,由此能求出实数a的取值范围.
解答 解:∵q:B={x∈R|x2-3x+2≤0}={x|1≤x≤2},
∵p是q的充分不必要条件,
条件p:A={x∈R|x2+ax+1=0},q:B={x∈R|x2-3x+2≤0}={x|1≤x≤2},
∴p⇒q,q不能推出p,即A是B的真子集,
∵可知A=∅或方程x2+ax+1=0的两根在区间[1,2]内,
∴△=a2-4<0,或$\left\{\begin{array}{l}{△={a}^{2}-4≥0}\\{1≤-\frac{a}{2}≤2}\\{f(1)=1+a+1≥0}\\{f(2)=4+2a+1≥0}\end{array}\right.$,解之可得-2≤a<2.
故实数a的取值范围为:[-2,2).
点评 本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意一元二次方程的根的性质的合理运用.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
5.已知向量$\overrightarrow{m}$=(sinA,$\frac{1}{2}$)与向量$\overrightarrow{n}$=(3,sinA+$\sqrt{3}$cosA)共线,其中A是△ABC的内角,则角A的大小为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
6.已知A(-1,0),B(2,0),平面内与点A距离为1,且与点B距离为2的直线的条数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
7.下列函数是奇函数的是( )
| A. | f(x)=x4 | B. | f(x)=x+$\frac{1}{x}$ | C. | f(x)=x3-1 | D. | f(x)=$\frac{1}{{x}^{2}}$ |
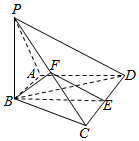 如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是棱CD和PC的中点.
如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是棱CD和PC的中点.