题目内容
已知a，b，c分别为△ABC三个内角A，B，C的对边，若cosB=
，a=10，△ABC的面积为42，则b+
的值等于（ ）
| 4 |
| 5 |
| a |
| sinA |
A、
| ||||
B、16
| ||||
C、8
| ||||
| D、16 |
考点：正弦定理
专题：解三角形
分析：由cosB的值及B为三角形的内角，利用同角三角函数间的基本关系求出sinB的值，利用三角形面积公式表示出三角形ABC面积，将a，sinA以及已知面积代入求出c的值，再利用余弦定理求出b的值，利用正弦定理求出
的值，即可确定出原式的值．
| a |
| sinA |
解答：
解：：∵cosB=
，B为三角形内角，∴sinB=
=
．
∵a=10，△ABC的面积为42，∴
ac•sinB=42，即3c=42，解得：c=14，
∴由余弦定理得：b2=a2+c2-2accosB=100+196-224=72，即b=6
．
再由正弦定理可得
=
=
=10
，∴b+
=16
，
故选：B．
| 4 |
| 5 |
| 1-cos2B |
| 3 |
| 5 |
∵a=10，△ABC的面积为42，∴
| 1 |
| 2 |
∴由余弦定理得：b2=a2+c2-2accosB=100+196-224=72，即b=6
| 2 |
再由正弦定理可得
| a |
| sinA |
| b |
| sinB |
6
| ||
|
| 2 |
| a |
| sinA |
| 2 |
故选：B．
点评：此题考查了正弦、余弦定理，以及三角形的面积公式，熟练掌握定理及公式是解本题的关键，属于基础题．
练习册系列答案
相关题目
已知某几何体的三视图如图所示（单位cm），则此几何体的体积为（ ）
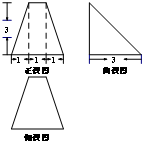
A、
| ||
B、
| ||
| C、16cm3 | ||
| D、12cm3 |
| a |
| a |
| b |
| a |
| b |
| 2 |
| b |
A、
| ||
B、
| ||
| C、5 | ||
| D、25 |
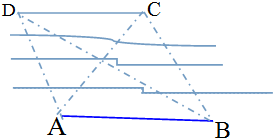如图所示，为了测量河对岸两个建筑物C，D两点之间的距离，在河岸这边选取点A，B，测得∠BAC=45°，∠DAC=75°，∠ABD=30°，∠DBC=45°，又已知AB=