题目内容
3．函数f（x）=cos（3x+φ）的图象关于原点成中心对称，则φ等于（ ）| A． | -$\frac{π}{2}$ | B． | 2kπ-$\frac{π}{2}$（k∈Z） | C． | kπ（k∈Z） | D． | kπ+$\frac{π}{2}$（k∈Z） |
分析 由题意可知f（0）=0，即cosφ=0，由此求φ得答案．
解答 解：∵f（x）=cos（3x+φ）的图象关于原点成中心对称，
∴当x=0时，f（x）=0，即cosφ=0，
∴φ=$kπ+\frac{π}{2}$，k∈Z．
故选：D．
点评 本题考查余弦函数的图象，考查函数奇偶性的性质，是基础题．
练习册系列答案
相关题目
14．通过随机询问100名性别不同的大学生是否爱好踢毽子，得到如的列联表，参照附表，则在犯错误概率不超过（ ）情况下认为“爱好该项运动与性别有关”．
| 男 | 女 | 总计 | |
| 爱好 | 10 | 40 | 50 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 30 | 70 | n |
| A． | 1% | B． | 2.5% | C． | 5% | D． | 10% |
15．《张丘建算经》卷上第22题为：“今有女善织，日益功疾（注：从第2天开始，每天比前一天多织相同量的布），第一天织5尺布，从第2天起每天比前一天多织$\frac{16}{29}$尺布，则一月（按30天计）共织（ ）尺布．
| A． | 250 | B． | 300 | C． | 360 | D． | 390 |
12．
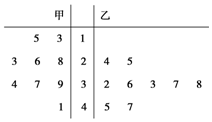如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图，甲、乙两人这几场比赛得分的平均数分别为$\overline{x_甲}$，$\overline{x_乙}$；准差分别是s甲，s乙，则有（ ）
如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图，甲、乙两人这几场比赛得分的平均数分别为$\overline{x_甲}$，$\overline{x_乙}$；准差分别是s甲，s乙，则有（ ）| A． | $\overline{x_甲}$＜$\overline{x_乙}$，s甲＜s乙 | B． | $\overline{x_甲}$＜$\overline{x_乙}$，s甲＞s乙 | ||
| C． | $\overline{x_甲}$＞$\overline{x_乙}$，s甲＜s乙 | D． | $\overline{x_甲}$＞$\overline{x_乙}$，s甲＞s乙 |