题目内容
已知函数f（x+
）=x+
，求f（x）的解析式．
| 1 |
| x |
| 1 |
| x |
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：通过换元法求出函数的表达式，注意定义域的范围．
解答：
解：令t=x+
，
当x＞0时，t≥2，
当x＜0时，t≤-2，
∴f（t）=t，t∈{t|t≥2，或t≤-2}，
即f（x）=x，x∈{x|x≥2，或x≤-2}．
| 1 |
| x |
当x＞0时，t≥2，
当x＜0时，t≤-2，
∴f（t）=t，t∈{t|t≥2，或t≤-2}，
即f（x）=x，x∈{x|x≥2，或x≤-2}．
点评：本题考查了函数的解析式的求法，换元法法的应用，定义域的确定，是一道基础题．
练习册系列答案
相关题目
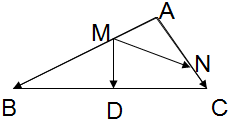如图：在△ABC中，D为BC中点，AM=
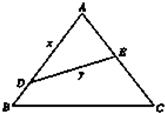如图，公园要把一块边长为2a的等边三角形ABC的边角地修成草坪，DE把草坪分成面积相等的两部分，D在AB上，E在AC上．