题目内容
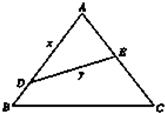 如图,公园要把一块边长为2a的等边三角形ABC的边角地修成草坪,DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
如图,公园要把一块边长为2a的等边三角形ABC的边角地修成草坪,DE把草坪分成面积相等的两部分,D在AB上,E在AC上.(1)设AD=x(x≥a),DE=y,试用x表示函数y;
(2)如果DE是灌溉水管,希望它最短,D、E的位置应该在哪里?
考点:函数模型的选择与应用
专题:应用题,不等式的解法及应用
分析:(1)在△ADE中,由余弦定理可得x,y,AE之间的关系,然后由S△ADE=
S△ABC,结合面积公式可求x与AE的关系,即可得到结论;
(2)利用基本不等式可求函数的最小值,即可得出结论.
| 1 |
| 2 |
(2)利用基本不等式可求函数的最小值,即可得出结论.
解答:
解:(1)在△ADE中,y2=x2+AE2-2x•AE•cos60°⇒y2=x2+AE2-x•AE,①…(2分)
又S△ADE=
S△ABC=x•AE•sin60°,
∴AE=
(4分)
②代入①得y=
(a≤x≤2a)…(8分)
(2)如果DE是水管y=
≥
a,…(12分)
当且仅当x2=
,即x=
a时“=”成立,…(13分)
故DE∥BC且AD=
a时水管的长度最短(15分)
又S△ADE=
| 1 |
| 2 |
∴AE=
| 2a2 |
| x |
②代入①得y=
x2+
|
(2)如果DE是水管y=
x2+
|
| 2 |
当且仅当x2=
| 4a4 |
| x2 |
| 2 |
故DE∥BC且AD=
| 2 |
点评:本题主要考查了余弦定理,三角形的面积公式在求解三角形中的应用,及基本不等式在函数的最值求解中的应用,计算虽然简单,但是考查的内容具有较强的综合性

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目