题目内容
已知定义在区间（0，+∞）上的函数f（x）满足f（
）=f（x1）-f（x2），且当x＞1时，f（x）＜0．
（1）求f（1）的值；
（2）判断函数f（x）的单调性．
| x1 |
| x2 |
（1）求f（1）的值；
（2）判断函数f（x）的单调性．
考点：抽象函数及其应用
专题：计算题,函数的性质及应用
分析：（1）由条件令x1=x2，则f（1）=0；（2）由单调性定义，设0＜x2＜x1，则
＞1，由x＞1时，f（x）＜0，
即有f（
）＜0，即可求得单调性．
| x1 |
| x2 |
即有f（
| x1 |
| x2 |
解答：
解：（1）∵f（x）满足f（
）=f（x1）-f（x2），
∴令x1=x2，则f（1）=0；
（2）定义在区间（0，+∞）上的函数f（x）为减函数，
理由如下：设0＜x2＜x1，
则
＞1，
∵x＞1时，f（x）＜0，∴f（
）＜0，
∴f（x1）-f（x2）＜0，即f（x1）＜f（x2），
∴函数f（x）在区间（0，+∞）上为减函数．
| x1 |
| x2 |
∴令x1=x2，则f（1）=0；
（2）定义在区间（0，+∞）上的函数f（x）为减函数，
理由如下：设0＜x2＜x1，
则
| x1 |
| x2 |
∵x＞1时，f（x）＜0，∴f（
| x1 |
| x2 |
∴f（x1）-f（x2）＜0，即f（x1）＜f（x2），
∴函数f（x）在区间（0，+∞）上为减函数．
点评：本题考查抽象函数及应用，考查函数的单调性，注意运用定义，同时考查解决抽象函数的常用方法：赋值法，属于基础题．
练习册系列答案
相关题目
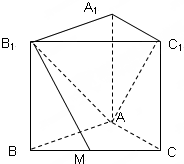如图，正三棱柱ABC-A1B1C1中，点M是BC的中点，AB=2，BB1=