题目内容
7.假设某种设备使用的年限x(年)与所支出的维修费用y(元)有以下统计资料:| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2 | 4 | 5 | 6 | 7 |
(1)求$\overline x,\overline y$;
(2)线性回归方程$\hat y=\hat bx+\hat a$;
(3)估计使用10年时,维修费用是多少?
(参考公式:$\hat b=\frac{{\sum_{i=1}^n{({x_i}}-\bar x)({y_i}-\bar y)}}{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\bar x\bar y}}{{\sum_{i=1}^n{{x_i}^2-n{{\bar x}^2}}}}$,$\hat a=\bar y-\hat b\bar x$)
分析 (1)利用$\overline{x}$,$\overline{y}$的计算公式即可得出.
(2)分别计算:$\sum_{i=1}^{5}{x}_{i}{y}_{i}$,$5\overline{x}\overline{y}$.$\sum_{i=1}^{5}{x}_{i}^{2}$,$5{\overline{x}}^{2}$,即可得出$\widehat{b}$,$\widehat{a}$=$\overline{y}-\widehat{b}\overline{x}$,及其$\widehat{y}$的解析式.
(3)代入(2)的解析式即可得出.
解答 解:(1)$\overline{x}$=$\frac{2+3+4+5+6}{5}$=4,$\overline{y}$=$\frac{2+4+5+6+7}{5}$=4.8.
(2)$\sum_{i=1}^{5}{x}_{i}{y}_{i}$=2×2+3×4+4×5+5×6+6×7=108,$5\overline{x}\overline{y}$=5×4×4.8=96.
$\sum_{i=1}^{5}{x}_{i}^{2}$=90,$5{\overline{x}}^{2}$=80,
∴$\widehat{b}$=$\frac{108-96}{90-80}$=1.2,$\widehat{a}$=$\overline{y}-\widehat{b}\overline{x}$=4.8-1.2×4=0,
∴$\widehat{y}$=1.2x.
(3)$当x=10时,\hat y=12$.
答:(1)$\overline{x}$=4,$\overline{y}$=4.8.
(2)$\widehat{b}$=1.2,$\widehat{a}$=0,$\widehat{y}$=1.2x.
(3)维修费用是12.
点评 本题考查了线性回归方程的计算公式,考查了推理能力与计算能力,属于中档题.

 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案| A. | M是N的真子集 | B. | N是M的真子集 | C. | M=N | D. | M∩N=φ |
| A. | 20 | B. | -20 | C. | 15 | D. | -15 |
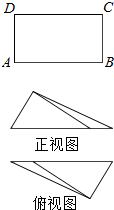 如图,在矩形ABCD中,$AB=\sqrt{3}$,BC=1,沿AC将矩形ABCD折叠,连接BD,所得三棱锥D-ABC的正视图和俯视图如图所示,则三棱锥D-ABC的侧视图的面积为( )
如图,在矩形ABCD中,$AB=\sqrt{3}$,BC=1,沿AC将矩形ABCD折叠,连接BD,所得三棱锥D-ABC的正视图和俯视图如图所示,则三棱锥D-ABC的侧视图的面积为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{4}$ |