题目内容
2.已知数列{an}的前n项和为Sn,且Sn+2=2an(n∈N*).(I)求数列{an}的通项公式;
(Ⅱ)设bn=log2an,数列{$\frac{1}{{{b_n}•{b_{n+1}}}}$}的前n项和为Tn,证明:Tn<1.
分析 (I)求得数列的首项,将n换为n-1,相减可得an=2an-1,运用等比数列的通项公式即可得到所求;
(Ⅱ)求得bn=log2an=n,$\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{n}$-$\frac{1}{n+1}$,再由数列的求和方法:裂项相消求和,以及不等式的性质,即可得证.
解答 解:(I)由Sn+2=2an,
当n=1时,a1+2=2a1,解得a1=2;
当n≥2时,Sn-1+2=2an-1有an=2an-2an-1,即an=2an-1,
所以数列{an}是以2为首项,2为公比的等比数列,
数列{an}的通项公式为an=2×2n-1=2n.
(Ⅱ)证明:由(I)得bn=log22n=n,
所以Tn=$\frac{1}{{b}_{1}{b}_{2}}$+$\frac{1}{{b}_{2}{b}_{3}}$+$\frac{1}{{b}_{3}{b}_{4}}$+…+$\frac{1}{{b}_{n}{b}_{n+1}}$
=$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n•(n+1)}$
=$\frac{1}{1}$-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$
=1-$\frac{1}{n+1}$<1.
点评 本题考查等差数列前n项和与通项公式的应用,裂项求和证明不等式问题,对逻辑推理能力和化归与转化思想都有所考查,难度中等.

练习册系列答案
相关题目
10.函数f(x)=$\frac{1}{\sqrt{2-x}}$+ln(1+x)的定义域是( )
| A. | (-2,-1) | B. | (-1,+∞) | C. | (-∞,+∞) | D. | (-1,2) |
17.已知数列{an}中a1=1,an+1=$\frac{a_n}{{3{a_n}+1}}$,则a34=( )
| A. | $\frac{34}{103}$ | B. | 100 | C. | $\frac{1}{100}$ | D. | $\frac{1}{104}$ |
7.假设某种设备使用的年限x(年)与所支出的维修费用y(元)有以下统计资料:
若由资料知y对x呈线性相关关系.试求:
(1)求$\overline x,\overline y$;
(2)线性回归方程$\hat y=\hat bx+\hat a$;
(3)估计使用10年时,维修费用是多少?
(参考公式:$\hat b=\frac{{\sum_{i=1}^n{({x_i}}-\bar x)({y_i}-\bar y)}}{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\bar x\bar y}}{{\sum_{i=1}^n{{x_i}^2-n{{\bar x}^2}}}}$,$\hat a=\bar y-\hat b\bar x$)
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2 | 4 | 5 | 6 | 7 |
(1)求$\overline x,\overline y$;
(2)线性回归方程$\hat y=\hat bx+\hat a$;
(3)估计使用10年时,维修费用是多少?
(参考公式:$\hat b=\frac{{\sum_{i=1}^n{({x_i}}-\bar x)({y_i}-\bar y)}}{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\bar x\bar y}}{{\sum_{i=1}^n{{x_i}^2-n{{\bar x}^2}}}}$,$\hat a=\bar y-\hat b\bar x$)
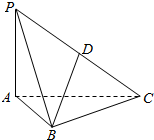 如图,PA⊥平面ABC,PA=$\sqrt{2}$,AB=1,BC=$\sqrt{3}$,AC=2,D是PC的中点.
如图,PA⊥平面ABC,PA=$\sqrt{2}$,AB=1,BC=$\sqrt{3}$,AC=2,D是PC的中点.