题目内容
19．直线l过抛物线y2=4x的焦点，与抛物线交于A，B两点，若|AB|=8，求直线l的方程．分析 求出抛物线y2=4x的焦点坐标为（1，0），通过若l与x轴垂直，求出|AB，设所求直线l的方程为y=k（x-1）．与抛物线联立，利用韦达定理通过抛物线的性质，求解直线方程即可．
解答 解：∵抛物线y2=4x的焦点坐标为（1，0），
若l与x轴垂直，则|AB|=4，不符合题意，
∴可设所求直线l的方程为y=k（x-1）．
代入抛物线方程化简可得：k2x2-（2k2+4）x+k2=0，
则由根与系数的关系，得x1+x2=$\frac{2k2+4}{k2}$．
又AB过焦点，由抛物线的定义可知|AB|=x1+x2+p=$\frac{2k2+4}{k2}$+2=8，
∴$\frac{2k2+4}{k2}$=6，解得k=±1．
∴所求直线l的方程为y+x-1=0或x-y-1=0．
点评 本题考查直线与抛物线的位置关系的应用，抛物线的简单性质的应用，考查计算能力以及转化思想的应用．
练习册系列答案
相关题目
7．下列函数表示同一函数的是（ ）
| A． | f（x）=x-2和g（x）=$\frac{{x}^{2}-4}{x+2}$ | B． | f（x）=x2和g（x）=$\frac{{x}^{4}}{x}$ | ||
| C． | f（x）=$\root{3}{{x}^{3}}$和g（x）=（$\sqrt{x}$）2 | D． | f（x）=4x2和g（m）=4m2 |
10．函数f（x）=$\frac{1}{\sqrt{2-x}}$+ln（1+x）的定义域是（ ）
| A． | （-2，-1） | B． | （-1，+∞） | C． | （-∞，+∞） | D． | （-1，2） |
7．假设某种设备使用的年限x（年）与所支出的维修费用y（元）有以下统计资料：
若由资料知y对x呈线性相关关系．试求：
（1）求$\overline x，\overline y$；
（2）线性回归方程$\hat y=\hat bx+\hat a$；
（3）估计使用10年时，维修费用是多少？
（参考公式：$\hat b=\frac{{\sum_{i=1}^n{（{x_i}}-\bar x）（{y_i}-\bar y）}}{{\sum_{i=1}^n{{{（{x_i}-\bar x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\bar x\bar y}}{{\sum_{i=1}^n{{x_i}^2-n{{\bar x}^2}}}}$，$\hat a=\bar y-\hat b\bar x$）
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2 | 4 | 5 | 6 | 7 |
（1）求$\overline x，\overline y$；
（2）线性回归方程$\hat y=\hat bx+\hat a$；
（3）估计使用10年时，维修费用是多少？
（参考公式：$\hat b=\frac{{\sum_{i=1}^n{（{x_i}}-\bar x）（{y_i}-\bar y）}}{{\sum_{i=1}^n{{{（{x_i}-\bar x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\bar x\bar y}}{{\sum_{i=1}^n{{x_i}^2-n{{\bar x}^2}}}}$，$\hat a=\bar y-\hat b\bar x$）
11．
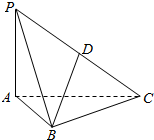如图，PA⊥平面ABC，PA=$\sqrt{2}$，AB=1，BC=$\sqrt{3}$，AC=2，D是PC的中点．
（1）求二面角B-PA-C的大小；
（2）求直线BD与平面ABC所成角的正切值．
如图，PA⊥平面ABC，PA=$\sqrt{2}$，AB=1，BC=$\sqrt{3}$，AC=2，D是PC的中点．（1）求二面角B-PA-C的大小；
（2）求直线BD与平面ABC所成角的正切值．
8．已知函数y=f（x）为奇函数且在R上的单调递增，若f（2m）+f（1-m）＞0，则实数m的取值范围是（ ）
| A． | （-1，2] | B． | （-1，+∞） | C． | （-1，4] | D． | [-1，+∞） |
9．“a=$\frac{1}{2}$”是“直线l1：（a+2）x+（a-2）y=1与直线l2：（a-2）x+（3a-4）y=2相互垂直”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |