题目内容
16.在平面直角坐标系中,以O为极点,x轴非负半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρsin2θ-4cosθ=0,直线l的参数方程为$\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{2}t-1}\\{y=\frac{\sqrt{3}}{2}t-3}\end{array}\right.$(t为参数).直线l与曲线C交于M、N两点.(1)写出曲线C的直角坐标方程和直线l的普通方程.
(2)求三角形OMN的面积.
分析 (1)曲线C的极坐标方程化为ρ2sin2θ=4ρcosθ,由此能求出曲线C的直角坐标方程,直线l的参数方程消去参数得直线l的普通方程.
(2)联立$\left\{\begin{array}{l}{{y}^{2}=4x}\\{x-y-2=0}\end{array}\right.$,得x2-8x+4=0,由此利用韦达定理、点到直线距离公式能求出三角形OMN的面积.
解答 解:(1)∵曲线C的极坐标方程为ρsin2θ-4cosθ=0,
∴ρ2sin2θ=4ρcosθ,
∴曲线C的直角坐标方程为y2=4x.
∵直线l的参数方程为$\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{2}t-1}\\{y=\frac{\sqrt{3}}{2}t-3}\end{array}\right.$(t为参数),
∴消去参数得直线l的普通方程为x-y-2=0.
(2)联立$\left\{\begin{array}{l}{{y}^{2}=4x}\\{x-y-2=0}\end{array}\right.$,消去y,得x2-8x+4=0,
∵直线l与曲线C交于M、N两点,
∴设M(x1,y1),N(x2,y2),则x1+x2=8,x1x2=4,
∴|MN|=$\sqrt{1+1}•\sqrt{{8}^{2}-4×4}$=4$\sqrt{6}$,
原点O到直线MN的距离d=$\frac{|0-0-2|}{\sqrt{2}}$=$\sqrt{2}$,
∴三角形OMN的面积S=$\frac{1}{2}×\sqrt{2}×4\sqrt{6}$=4$\sqrt{3}$.
点评 本题考查曲线的直角坐标方程和直线的参数方程的求法,考查三角形面积的求法,是中档题,解题时要认真审题,注意点到直线的距离公式的合理运用.

 金钥匙试卷系列答案
金钥匙试卷系列答案| A. | 2 | B. | ±2 | C. | $\frac{5}{2}$ | D. | 5 |
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2 | 4 | 5 | 6 | 7 |
(1)求$\overline x,\overline y$;
(2)线性回归方程$\hat y=\hat bx+\hat a$;
(3)估计使用10年时,维修费用是多少?
(参考公式:$\hat b=\frac{{\sum_{i=1}^n{({x_i}}-\bar x)({y_i}-\bar y)}}{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\bar x\bar y}}{{\sum_{i=1}^n{{x_i}^2-n{{\bar x}^2}}}}$,$\hat a=\bar y-\hat b\bar x$)
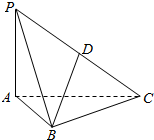 如图,PA⊥平面ABC,PA=$\sqrt{2}$,AB=1,BC=$\sqrt{3}$,AC=2,D是PC的中点.
如图,PA⊥平面ABC,PA=$\sqrt{2}$,AB=1,BC=$\sqrt{3}$,AC=2,D是PC的中点.(1)求二面角B-PA-C的大小;
(2)求直线BD与平面ABC所成角的正切值.
| A. | {x|-1≤x<5} | B. | {x|4<x<5} | C. | {x|1<x<5} | D. | {x|-1<x<1} |
| A. | (-1,2] | B. | (-1,+∞) | C. | (-1,4] | D. | [-1,+∞) |