题目内容
若(
+x)2n=a0+a1x+…+a2nx2n,则
[(a0+a2+…+a2n)2}-(a1+a3+…+a2n-1)2]=( )
| ||
| 2 |
| lim |
| n→∞ |
| A、1 | ||||
B、
| ||||
| C、0 | ||||
| D、-1 |
考点:二项式定理的应用
专题:二项式定理
分析:因为求极限的数为二项式展开式的奇数项的系数和的平方与偶数项的系数和的平方的差,故可以赋值x=1代入二项展开式中A=(
+1)2n=a0+a1+…+a2n;x=-1可得,B=(
-1)2n=a0-a1+a2-a3+…-a2n-1+a2n,而求极限的数由平方差公式可以知道就是式子A与B的乘积,代入后由平方差公式即可化简为求得答案.
| ||
| 2 |
| ||
| 2 |
解答:
解:令x=1得,A=(
+1)2n=a0+a1+…+a2n;x=-1可得,B=(
-1)2n=a0-a1+a2-a3+…-a2n-1+a2n,
所以(a0+a2+…+a2n)2-(a1+a3+…+a2n-1)2
=(a0+a1+…+a2n)(a0-a1+…-a2n-1)
=(
+1)2n(
-1)2n
=[(
+1)(
-1)]2n
=(
)2n=
;
∴
[(a0+a2+a4+…+a2n)2-(a1+a3+a5…+a2n-1)2]=
=0.
故选C.
| ||
| 2 |
| ||
| 2 |
所以(a0+a2+…+a2n)2-(a1+a3+…+a2n-1)2
=(a0+a1+…+a2n)(a0-a1+…-a2n-1)
=(
| ||
| 2 |
| ||
| 2 |
=[(
| ||
| 2 |
| ||
| 2 |
=(
| 1 |
| 2 |
| 1 |
| 4n |
∴
| lim |
| n→∞ |
| lim |
| n→∞ |
| 1 |
| 4n |
故选C.
点评:本题主要考查了二项式定理的应用,主要是二项式系数和差的考查,对于二项式系数的问题常常常用赋值法解决;同时还考查了学生的计算能力与转化能力以及求极限问题.

练习册系列答案
相关题目
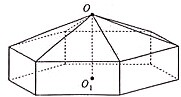 请您设计一个帐篷,它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积为16
请您设计一个帐篷,它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积为16