题目内容
定义:若
在[k,+∞)上为增函数,则称h(x)为“k次比增函数”,其中k∈N*,已知f(x)=x3+2ax2+ax,g(x)=ex-ax.
(Ⅰ)若f(x)是“1次比增函数”,又是“2次比增函数”,求实数a的取值范围;
(Ⅱ)当a=1时,求函数g(x)在[m-1,m](m>0)上的最小值.
| h(x) |
| xk |
(Ⅰ)若f(x)是“1次比增函数”,又是“2次比增函数”,求实数a的取值范围;
(Ⅱ)当a=1时,求函数g(x)在[m-1,m](m>0)上的最小值.
考点:利用导数研究函数的单调性
专题:探究型,导数的综合应用
分析:(1)应用条件f(x)是“1次比增函数”,又是“2次比增函数”,得出函数的单调性,再用导数推理,
(2)先探讨函数g(x)的单调性,再对m进行分类讨论.
(2)先探讨函数g(x)的单调性,再对m进行分类讨论.
解答:
解:(1)∵f(x)是“1次比增函数”,
∴
=x2+2ax+a在[1,+∞)上为增函数,
∴-a≤1,∴a≥-1,
∵f(x)是“2次比增函数”,则
=x+
+2a在[2,+∞)为增函数,
则(x+
+2a)′=1-
≥0在[2,+∞)恒成立,
∴a≤x2在[2,+∞)恒成立,∴a≤4,
综上a的取值范围为[-1,4].
(2)当a=1时,函数g(x)=ex-x
g′(x)=ex-1,
由g′(x)>0,得x>0;由g′(x)<0,得x<0,
∴g(x)在(-∞,0)单调递减,在(0,+∞)单调递增,
①当m-1<0<m,即0<m<1时,g(x)在[m-1,0]上单调递减,在[0,m]上单调递增,
∴g(x)min=g(0)=1,
②当m-1≥0,即m≥0时,g(x)在[m-1,m]上单调递增,
∴g(x)min=g(m-1)=em-1-m+1.
综上,当m-1<0<m,g(x)min=1,
当m≥0时,∴g(x)min=g(m-1)=em-1-m+1.
∴
| f(x) |
| x |
∴-a≤1,∴a≥-1,
∵f(x)是“2次比增函数”,则
| f(x) |
| x2 |
| a |
| x |
则(x+
| a |
| x |
| a |
| x2 |
∴a≤x2在[2,+∞)恒成立,∴a≤4,
综上a的取值范围为[-1,4].
(2)当a=1时,函数g(x)=ex-x
g′(x)=ex-1,
由g′(x)>0,得x>0;由g′(x)<0,得x<0,
∴g(x)在(-∞,0)单调递减,在(0,+∞)单调递增,
①当m-1<0<m,即0<m<1时,g(x)在[m-1,0]上单调递减,在[0,m]上单调递增,
∴g(x)min=g(0)=1,
②当m-1≥0,即m≥0时,g(x)在[m-1,m]上单调递增,
∴g(x)min=g(m-1)=em-1-m+1.
综上,当m-1<0<m,g(x)min=1,
当m≥0时,∴g(x)min=g(m-1)=em-1-m+1.
点评:本题主要考查函数与导数的关系,且此题也是一个创新题,读懂题目中的概念是解题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
已知函数f(x)=x2+ln(x+m)与函数g(x)=x2+ex-
(x<0)的图象上存在关于y轴对称的点(e为自然对数的底数),则m的取值范围是( )
| 1 |
| 2 |
A、(-∞,
| ||||||
B、(-∞,
| ||||||
C、(-
| ||||||
D、(-
|
函数f(x)=|log2(x+1)|的图象大致是( )
A、 |
B、 |
C、 |
D、 |
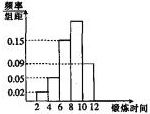 某校友200位教职员工,其每周用于锻炼身体所用时间的频率分布直方图如图所示,据图估计,锻炼时间在[8,10]小时内的人数为( )
某校友200位教职员工,其每周用于锻炼身体所用时间的频率分布直方图如图所示,据图估计,锻炼时间在[8,10]小时内的人数为( )| A、76 | B、82 | C、88 | D、95 |