题目内容
已知函数f（x）=
定义域为M，集合N={x|x2-2x=0}，则M∩N=（ ）
| 1-x |
| A、{0，2} | B、{0} |
| C、{2} | D、∅ |
考点：交集及其运算
专题：集合
分析：求解函数定义域化简集合M，求解方程化简集合N，然后直接利用交集运算求解．
解答：
解：由1-x≥0，得x≤1．
∴M={x|x≤1}，
N={x|x2-2x=0}={0，2}，
∴M∩N={0}．
故选：B．
∴M={x|x≤1}，
N={x|x2-2x=0}={0，2}，
∴M∩N={0}．
故选：B．
点评：本题考查了交集及其运算，考查了函数定义域的求法，是基础题．
练习册系列答案
相关题目
在数列{an}中，a1=3，an+1=an+lg（1+
）（n∈N*），则an=（ ）
| 1 |
| n |
| A、lgn | ||||||
B、3+lg（
| ||||||
| C、3+lgn | ||||||
| D、3+3lng |
若函数f（x）=2x3-9x2+12x-a恰好有两上不同零点，则a的值为（ ）
| A、4 | B、5或6 |
| C、4或5 | D、4或6 |
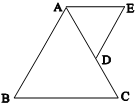如图所示，等边△ABC的边长为2，D为AC中点，且△ADE也是等边三角形，在△ADE以点A为中心向下转动到稳定位置的过程中，| BD |
| CE |
A、[
| ||||
B、[
| ||||
C、（
| ||||
D、（
|