题目内容
已知曲线y=x3,直线l是过点(1,1)且与曲线相切的直线,则直线l的方程是( )
| A、3x-y-2=0 |
| B、3x-4y+1=0 |
| C、3x-y-2=0或x-y=0 |
| D、3x-y-2=0或3x-4y+1=0 |
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:求出函数的导数,结合直线关系即可得到结论.
解答:
解:函数的导数为f′(x)=3x2,
设切点为(a,b),
则k=f′(a)=3a2,b=a3,
则切线的方程y-b=3a2(x-a),
即y=3a2x-2a3,
∵直线l过点(1,1),
∴3a2x-2a3=1,
即2a3-3a2+1=0,
则(a-1)(2a2-a-1)=0,
则(a-1)2(2a+1)=0,
解得a=1或a=-
,
当a=1时,对应的直线方程为y=3x-2,即3x-y-2=0,
当a=-
时,对应的直线方程为y=
x+
,即3x-4y+1=0,
故选:C
设切点为(a,b),
则k=f′(a)=3a2,b=a3,
则切线的方程y-b=3a2(x-a),
即y=3a2x-2a3,
∵直线l过点(1,1),
∴3a2x-2a3=1,
即2a3-3a2+1=0,
则(a-1)(2a2-a-1)=0,
则(a-1)2(2a+1)=0,
解得a=1或a=-
| 1 |
| 2 |
当a=1时,对应的直线方程为y=3x-2,即3x-y-2=0,
当a=-
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 4 |
故选:C
点评:本题主要考查函数的切线的求解,根据函数导数的几何意义是解决本题的关键.

练习册系列答案
相关题目
(理科)已知-3<a<2,3<b<4,则
的取值范围为( )
| a |
| b |
A、(-1,
| ||||
B、(-
| ||||
C、(-1,
| ||||
D、(-
|
今年4月20日8:30分四川芦山发生强地震,得知此消息,某医院决定从4名内科和6名外科医生(包含一名骨外科专家)10名医生中,用分层抽样的方式组成一个5人的医疗小组赶赴灾区展开震后的救护工作,则骨外科专家被选派的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
4月20日四川庐山发生7.0级,某地区医疗队知道此消息后准备从5个内科医生和4个外科医生中选派5人去参加救援,其中外科医生至少要派3人参加,则一共有( )种选派方法.
| A、126 | B、80 | C、60 | D、45 |
已知圆柱的底面半径为2,高为3,用一个平面去截,若所截得的截面为椭圆,则椭圆的离心率的取值范围为( )
A、[
| ||
B、(0,
| ||
C、[
| ||
D、(0,
|
已知f1(x)=sinx-cosx,fn+1(x)是fn(x)的导函数,即f2(x)=f1′(x),f3(x)=f2′(x),…,fn+1(x)=fn′(x),n∈N*,则f2013(x)=( )
| A、sinx+cosx |
| B、sinx-cosx |
| C、-sinx+cosx |
| D、-sinx-cosx |
在极坐标系中,圆C的圆心为(6,
),半径为5,直线θ=α(0≤α≤
,ρ∈R)被圆截得的弦长为8,则α的值为( )
| π |
| 2 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
| D、以上都不对 |
设A=
,B=
,则A与B的大小关系是( )
| x+1 |
| x+2 |
| x+3 |
| x+4 |
| A、A<B |
| B、A>B |
| C、仅有x>0,A<B |
| D、以上结论都不成立 |
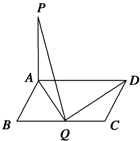 如图所示,已知矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥QD,则a=( )
如图所示,已知矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥QD,则a=( )