题目内容
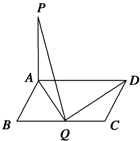 如图所示,已知矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥QD,则a=( )
如图所示,已知矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥QD,则a=( )| A、1 | B、2 | C、3 | D、4 |
考点:直线与平面垂直的性质
专题:空间位置关系与距离
分析:利用三垂线定理的逆定理、直线与圆相切的判定与性质、矩形的性质、平行线的性质即可求出.
解答:
解:连接AQ,取AD的中点O,连接OQ.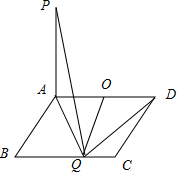
∵PA⊥平面ABCD,PQ⊥DQ,
由三垂线定理的逆定理可得DQ⊥AQ.
∴点Q在以线段AD的中点O为圆心的圆上,
又∵在BC上有且仅有一个点Q满足PQ⊥DQ,∴BC与圆O相切,(否则相交就有两点满足垂直,矛盾.)
∴OQ⊥BC,
∵AD∥BC,∴OQ=AB=1,∴BC=AD=2.
故选B.

∵PA⊥平面ABCD,PQ⊥DQ,
由三垂线定理的逆定理可得DQ⊥AQ.
∴点Q在以线段AD的中点O为圆心的圆上,
又∵在BC上有且仅有一个点Q满足PQ⊥DQ,∴BC与圆O相切,(否则相交就有两点满足垂直,矛盾.)
∴OQ⊥BC,
∵AD∥BC,∴OQ=AB=1,∴BC=AD=2.
故选B.
点评:本题体现转化的数学思想,转化为以AD为直径的圆与边BC有交点,熟练掌握三垂线定理的逆定理、直线与圆相切的判定与性质、矩形的性质、平行线的性质是解题的关键.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
| C | 1 33 |
| C | 2 33 |
| C | 3 33 |
| C | 33 33 |
| A、0 | B、11 | C、2 | D、7 |
有7个物体分三列用细绳栓在一根横杆上,每列分别栓2个,2个,3个.按如下规则向物体射击(假设每一轮均击中):每次先选择一列,然后向该列的最下端物体射击,直至7个物体全部命中.则不同的射击顺序( )种.
| A、210 | B、240 |
| C、264 | D、188 |
过抛物线y2=8x的焦点F作倾斜角是
π的直线,交抛物线与A,B两点,则|AB|=( )
| 3 |
| 4 |
| A、16 | ||
B、16
| ||
| C、8 | ||
D、8
|
已知
和
是两个单位向量,夹角是60°,则向量2
+
和-3
+2
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、90° | B、60° |
| C、120° | D、45° |
若复数Z满足
=2i,则
对应点位于( )
| z |
| 1+i |
. |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知曲线y=x3,直线l是过点(1,1)且与曲线相切的直线,则直线l的方程是( )
| A、3x-y-2=0 |
| B、3x-4y+1=0 |
| C、3x-y-2=0或x-y=0 |
| D、3x-y-2=0或3x-4y+1=0 |
△ABC中,若cosC=2sinAsinB-1则△ABC的形状一定是( )
| A、直角三角形 |
| B、等边三角形 |
| C、等腰直角三角形 |
| D、等腰三角形 |
点P是双曲线
-
=1上的一点,F1和F2分别是双曲线的左、右焦点,
•
=0,则△F1PF2的面积是( )
| x2 |
| 4 |
| y2 |
| 12 |
| PF1 |
| PF2 |
| A、24 | B、16 | C、8 | D、12 |