题目内容
4．
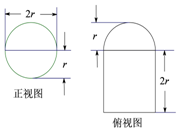圆柱被一个平面截去一部分后与半球（半径为 r ）组成一个几何体，该几何体的三视图中的正视图和俯视图如图所示，当r=5时，该几何体的表面积为（ ）| A． | 32+80π | B． | 64+40$\sqrt{2}$π | C． | 64+80π | D． | 100+125π |
分析 由几何体三视图中的正视图和俯视图知，该几何体是一个半球拼接半个圆柱，结合图中数据求出它的表面积．
解答 解：由几何体三视图中的正视图和俯视图可知，
截圆柱的平面过圆柱的轴线，
该几何体是一个半球拼接半个圆柱，
其表面积为：
$\frac{1}{2}$×4πr2+$\frac{1}{2}$×πr2+$\frac{1}{2}$×2r×2πr+2r×2r+$\frac{1}{2}$×πr2=5πr2+4r2
=100+125π．
故选：D．
点评 本题考查了根据几何体三视图求表面积的应用问题，是基础题．
练习册系列答案
相关题目
15．已知直线y=$\frac{2\sqrt{5}}{5}$x与双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）交于A、B两点，若在双曲线上存在点P，使得|PA|=|PB|=$\frac{\sqrt{3}}{2}$|AB|，则双曲线的离心率为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $\frac{\sqrt{5}}{2}$ | D． | $\sqrt{5}$ |
9．已知点A的坐标为A（1，1，0），向量$\frac{1}{2}$$\overrightarrow{AB}$=（4，0，2），则点B的坐标为（ ）
| A． | （7，-1，4） | B． | （9，1，4） | C． | （3，1，1） | D． | （1，-1，1） |