题目内容
13.设函数$f(x)=\frac{x}{x+2}(x>0)$,观察:${f_1}(x)=f(x)=\frac{x}{x+2}$,${f_2}(x)=f({f_1}(x))=\frac{x}{3x+4}$,${f_3}(x)=f({f_2}(x))=\frac{x}{7x+8}$,${f_4}(x)=f({f_3}(x))=\frac{x}{15x+16}$,…,根据以上事实,当n∈N*时,由归纳推理可得:fn(1)=$\frac{1}{{{2^{n+1}}-1}}$.分析 根据已知中函数的解析式,归纳出函数解析中分母系数的变化规律,进而得到答案.
解答 解:由${f_1}(x)=f(x)=\frac{x}{x+2}$,${f_2}(x)=f({f_1}(x))=\frac{x}{3x+4}$,${f_3}(x)=f({f_2}(x))=\frac{x}{7x+8}$,${f_4}(x)=f({f_3}(x))=\frac{x}{15x+16}$,…
归纳可得:fn(x)=$\frac{x}{({2}^{n}-1)x+{2}^{n}}$,(n∈N*)
∴fn(1)=$\frac{1}{{{2^{n+1}}-1}}$.
故答案为$\frac{1}{{{2^{n+1}}-1}}$.
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
3.直线$\sqrt{3}x+3y+a=0$的倾斜角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
4.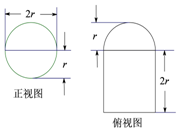 圆柱被一个平面截去一部分后与半球(半径为 r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,当r=5时,该几何体的表面积为( )
圆柱被一个平面截去一部分后与半球(半径为 r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,当r=5时,该几何体的表面积为( )
 圆柱被一个平面截去一部分后与半球(半径为 r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,当r=5时,该几何体的表面积为( )
圆柱被一个平面截去一部分后与半球(半径为 r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,当r=5时,该几何体的表面积为( )| A. | 32+80π | B. | 64+40$\sqrt{2}$π | C. | 64+80π | D. | 100+125π |
8.已知几何体的三视图如图所示,则该几何体的表面积是( )
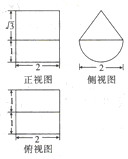

| A. | $2π+16+2\sqrt{3}$ | B. | $3π+16+2\sqrt{3}$ | C. | $3π+8+\sqrt{3}$ | D. | $3π+8+2\sqrt{3}$ |
3.若复数z满足$\frac{1+2i}{z}$=1-i,则复数z在复平面对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |