题目内容
19.参数方程$\left\{\begin{array}{l}x=-1+2cosθ\\ y=2+2sinθ\end{array}\right.$(θ为参数0≤θ<2π)所表示的曲线的普通方程是(x+1)2+(y-2)2=4.分析 由cos2θ+sin2θ=1,能求出曲线的普通方程.
解答 解:∵参数方程$\left\{\begin{array}{l}x=-1+2cosθ\\ y=2+2sinθ\end{array}\right.$(θ为参数0≤θ<2π),
∴$\left\{\begin{array}{l}{2cosθ=(x+1)}\\{2sinθ=y-2}\end{array}\right.$,(θ为参数0≤θ<2π),
∵cos2θ+sin2θ=1,
∴曲线的普通方程是(x+1)2+(y-2)2=4
故答案为:(x+1)2+(y-2)2=4.
点评 本题考查曲线的普通方程的求法,考查参数方程、普通方程的互化,考查推理论证能力、运算求解能力,考查转化化归思想、数形结合思想,是基础题.

练习册系列答案
相关题目
9.一个几何体的三视图如图所示,则这个几何体外接球体积与该几何体的体积比为( )


| A. | $\frac{3\sqrt{3}}{2}$π | B. | $\frac{\sqrt{3}}{4}$π | C. | $\frac{3\sqrt{3}}{4}$π | D. | $\frac{\sqrt{3}}{8}$π |
10.某三棱锥的三视图如图所示,其侧(左)视图为直角三角形,则该三棱锥外接球的表面积为( )


| A. | 50π | B. | 50$\sqrt{2}$π | C. | 40π | D. | 40$\sqrt{2}$π |
14.极坐标方程$sinθ=\frac{{\sqrt{2}}}{2}(ρ∈R)$表示的曲线是( )
| A. | 两条相交直线 | B. | 两条射线 | C. | 一条直线 | D. | 一条射线 |
4.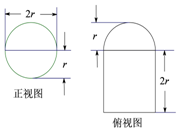 圆柱被一个平面截去一部分后与半球(半径为 r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,当r=5时,该几何体的表面积为( )
圆柱被一个平面截去一部分后与半球(半径为 r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,当r=5时,该几何体的表面积为( )
 圆柱被一个平面截去一部分后与半球(半径为 r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,当r=5时,该几何体的表面积为( )
圆柱被一个平面截去一部分后与半球(半径为 r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,当r=5时,该几何体的表面积为( )| A. | 32+80π | B. | 64+40$\sqrt{2}$π | C. | 64+80π | D. | 100+125π |
8.已知几何体的三视图如图所示,则该几何体的表面积是( )
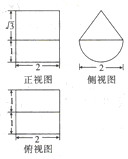

| A. | $2π+16+2\sqrt{3}$ | B. | $3π+16+2\sqrt{3}$ | C. | $3π+8+\sqrt{3}$ | D. | $3π+8+2\sqrt{3}$ |
 在空间四边形ABCD中,H,G分别是AD,CD的中点,E,F分别边AB,BC上的点,且$\frac{CF}{FB}$=$\frac{AE}{EB}$=$\frac{1}{3}$.求证:
在空间四边形ABCD中,H,G分别是AD,CD的中点,E,F分别边AB,BC上的点,且$\frac{CF}{FB}$=$\frac{AE}{EB}$=$\frac{1}{3}$.求证: