题目内容
14.已知函数f(x)=x2+(m-1)x+1(1)当m>0且f(x)的最小值为-3时,求m的值,并写出此时f(x)的单调区间
(2)若函数f(x)在区间[0,2]上有零点,求实数m的取值范围.
分析 (1)表示出f(x)的最小值,得到关于m的方程,解出m的值,求出函数的单调区间即可;
(2)当m=0时,经检验不满足条件.当f(x)在[0,2]上有一个零点时,求出m的值.当f(x)在[0,2]上有两个零点时,求出m的取值范围,再取并集即得所求.
解答 解:(1)f(x)的最小值是$\frac{4{-(m-1)}^{2}}{4}$=-3,解得:m=5;
故f(x)=x2+4x+1,对称轴是x=-2,
故f(x)在(-∞,-2)递减,在(-2,+∞)递增;
(2)当m=0时,函数f(x)=x2-x+1,在区间[0,2]上没有零点,不满足条件,故舍去.
当f(x)在[0,2]上有一个零点时,此时①$\left\{\begin{array}{l}{△{=(m-1)}^{2}-4=0}\\{0≤-\frac{m-1}{2}≤2}\end{array}\right.$,或 ②$\left\{\begin{array}{l}{△{=(m-1)}^{2}-4>0}\\{f(0)•f(2)<0}\end{array}\right.$成立,
解①得 m=-1,解②得 m<-$\frac{3}{2}$,
当f(x)在[0,2]上有两个零点时,此时 $\left\{\begin{array}{l}{△{=(m-1)}^{2}-4>0}\\{0≤-\frac{m-1}{2}≤2}\\{f(0)≥0}\\{f(2)≥0}\end{array}\right.$,解得-$\frac{3}{2}$≤m<-1,
综上可得,实数m的取值范围[-∞,-1].
点评 本题考查二次函数与方程之间的关系,二次函数在给定区间上的零点问题,要注意函数图象与x轴相切的情况,属于中档题.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
5.空间几何体的三视图如图所示,则该几何体的体积为( )
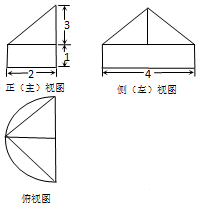

| A. | 4+2π | B. | 12+2π | C. | 4+4π | D. | 12+4π |
9.一个几何体的三视图如图所示,则这个几何体外接球体积与该几何体的体积比为( )


| A. | $\frac{3\sqrt{3}}{2}$π | B. | $\frac{\sqrt{3}}{4}$π | C. | $\frac{3\sqrt{3}}{4}$π | D. | $\frac{\sqrt{3}}{8}$π |
6.若一个正六棱柱(底面是正六边形,侧棱垂直于底面)的正视图如图所示,则其体积等于( )

| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{3\sqrt{3}}{2}$ | C. | 2$\sqrt{3}$ | D. | 6$\sqrt{3}$ |
3.直线$\sqrt{3}x+3y+a=0$的倾斜角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
4.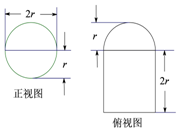 圆柱被一个平面截去一部分后与半球(半径为 r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,当r=5时,该几何体的表面积为( )
圆柱被一个平面截去一部分后与半球(半径为 r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,当r=5时,该几何体的表面积为( )
 圆柱被一个平面截去一部分后与半球(半径为 r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,当r=5时,该几何体的表面积为( )
圆柱被一个平面截去一部分后与半球(半径为 r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,当r=5时,该几何体的表面积为( )| A. | 32+80π | B. | 64+40$\sqrt{2}$π | C. | 64+80π | D. | 100+125π |
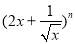 的展开式前两项的二项式系数之和为10.
的展开式前两项的二项式系数之和为10.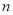 的值.
的值.