题目内容
椭圆的焦点在x轴上,离心率为
,且椭圆被直线y=x+2截得的线段长为
,求椭圆的标准方程.
| ||
| 2 |
16
| ||
| 5 |
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:椭圆的焦点在x轴上,可设椭圆的标准方程为
+
=1(a>b>0).由于椭圆的离心率为
,可得
=
,
由于a2=b2+c2.可得a2=4b2.椭圆的方程化为x2+4y2=4b2.与直线的方程联立,利用弦长公式即可得出.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| c |
| a |
| ||
| 2 |
由于a2=b2+c2.可得a2=4b2.椭圆的方程化为x2+4y2=4b2.与直线的方程联立,利用弦长公式即可得出.
解答:
解:∵椭圆的焦点在x轴上,
∴可设椭圆的标准方程为
+
=1(a>b>0).
∵椭圆的离心率为
,∴
=
,
∴a2=b2+c2=b2+
a2,化为a2=4b2.
∴椭圆的方程化为x2+4y2=4b2.
设直线与椭圆的交点A(x1,y1),B(x2,y2).
联立
化为5x2+16x+16-4b2=0,
△>0化为b2>
.
∴x1+x2=-
,x1x2=
.
∴|AB|=
=
=
,
化为b2=4.满足△>0.
∴椭圆的标准方程为:
+
=1.
∴可设椭圆的标准方程为
| x2 |
| a2 |
| y2 |
| b2 |
∵椭圆的离心率为
| ||
| 2 |
| c |
| a |
| ||
| 2 |
∴a2=b2+c2=b2+
| 3 |
| 4 |
∴椭圆的方程化为x2+4y2=4b2.
设直线与椭圆的交点A(x1,y1),B(x2,y2).
联立
|
△>0化为b2>
| 4 |
| 5 |
∴x1+x2=-
| 16 |
| 5 |
| 16-4b2 |
| 5 |
∴|AB|=
| 2[(x1+x2)2-4x1x2] |
2(
|
16
| ||
| 5 |
化为b2=4.满足△>0.
∴椭圆的标准方程为:
| x2 |
| 16 |
| y2 |
| 4 |
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、弦长公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
某几何体的三视图,如图所示,则这个几何体是( )


| A、三棱锥 | B、三棱柱 |
| C、四棱锥 | D、四棱柱 |
若点P(m,n)Q(n-1,m+1)关于直线l对称,则l的方程是( )
| A、x-y+1=0 |
| B、x-y=0 |
| C、x+y+1=0 |
| D、x+y=0 |
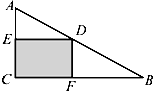 在RT△ABC中,直角边AC=3,BC=4,点D是斜边AB上的动点,DE⊥AC交AC于点E,DF⊥BC交BC于点F,设CE=x.
在RT△ABC中,直角边AC=3,BC=4,点D是斜边AB上的动点,DE⊥AC交AC于点E,DF⊥BC交BC于点F,设CE=x.