题目内容

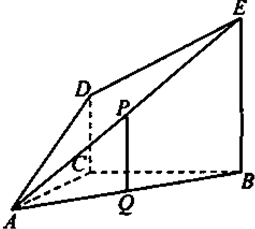
在△ABC中，角A、B、C的对边长分别为a、b、c，且a=3，b=2，A=2B，求cosB和c的值．
考点：余弦定理的应用
专题：计算题,解三角形
分析：利用正弦定理，求出cosB=
3
4
，再用余弦定理求出c的值．
解答： 解：∵A=2B，
a
sinA
=
b
sinB
，a=3，b=2，
∴
3
2sinBcosB
=
2
sinB
，
∴cosB=
3
4
，
∴
9+c2-4
6c
=
3
4
，
∴2c2-9c+10=0，
∴c=2或2.5，
因为c=2，不合题意舍去，所以c=
5
2
…（10分）
点评：本题主要考查了正弦定理和余弦定理的应用．在解三角形问题中，常需要用正弦定理和余弦定理完成边角互化，来解决问题．
练习册系列答案
相关题目
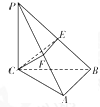如图，已知三棱锥P-ABC中，PC⊥平面ABC，AB⊥BC，PC=BC=4，AB=2，E、F分别是PB、PA的中点．
（1）求证：侧面PAB⊥侧面PBC；
（2）求三棱锥P-CEF的外接球的表面积．
已知函数f（x）=log2（2x+1）-kx为偶函数．
（1）求实数k的值；
（2）求证：f（x）在（0，+∞）上为增函数；
（3）若?t∈R，都有f（t2+2t+3）＞f（m），求实数m的取值范围．
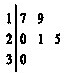某车间共有12名工人，随机抽取6名，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数．
（1）若日加工零件个数大于样本均值的工人为优秀工人，根据茎叶图推断该车间12名工人中有几名优秀工人？
（2）从这6名工人中任取2人，设这两人加工零件的个数分别为x、y，求|x-y|≤2的概率．
等比数列an中的前三项a1，a2，a3分别是下面数阵中第一、二、三行中的某三个数，且三个数不在同一列．
543
6108
20126

（1）求此数列{an}的通项公式；
（2）若数列{bn}满足bn=3an-（-1）nlgan，求数列{bn}的前n项和Sn．
如图，DC⊥平面ABC，EB∥DC，AC=BC=EB=2DC=2，P，Q分别为AE，AB的中点．

（Ⅰ）证明：PQ∥平面ACD；
（Ⅱ）证明：平面ADE⊥平面ABE．
定长为3的线段AB的两个端点A、B分别在x轴、y轴上滑动，动点P满足
BP
=2
PA
．
（Ⅰ）求点P的轨迹曲线C的方程；
（Ⅱ）若过点（1，0）的直线与曲线C交于M、N两点，求
OM
•
ON
的最大值．
曲线y=-ex在点A处的切线与直线x-y+3=0垂直，则点A的坐标是
 
．
设函数f（x）的定义域为D，若存在非零实数h，使得对于任意x∈M（M⊆D），有x+h∈D，且f（x+h）≥f（x），则称f（x）为M上的“h阶高调函数”．给出如下结论：
①若函数f（x）在R上单调递增，则存在非零实数h使f（x）为R上的“h阶高调函数”；
②若函数f（x）为R上的“h阶高调函数”，则f（x）在R上单调递增；
③若函数f（x）=x2为区间[-1，+∞）上的“h阶高调函数”，则h≥2；
④若函数f（x）在R上的奇函数，且x≥0时，f（x）=|x-1|-1，则f（x）只能是R上的“4阶高调函数”．
其中正确结论的序号为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网