题目内容
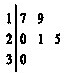 某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.(1)若日加工零件个数大于样本均值的工人为优秀工人,根据茎叶图推断该车间12名工人中有几名优秀工人?
(2)从这6名工人中任取2人,设这两人加工零件的个数分别为x、y,求|x-y|≤2的概率.
考点:茎叶图,古典概型及其概率计算公式
专题:概率与统计
分析:(1)根据茎叶图中的数据求出样本均值
,求出样本的优秀率并估计12名工人中优秀工人数;
(2)列出6人中任取2人,加工的零件个数的基本事件数,再求出满足|x-y|≤2的事件数,从而求出对应的概率.
. |
| x |
(2)列出6人中任取2人,加工的零件个数的基本事件数,再求出满足|x-y|≤2的事件数,从而求出对应的概率.
解答:
解:(1)样本均值为
=
(17+19+20+21+25+30)=22,
样本中大于22的有2人,∴样本的优秀率为
=
,
∴12名工人中优秀工人为12×
=4人;
(2)6人中任取2人,加工的零件个数构成基本事件:
(17,19),(17,20),(17,25),(17,30);
(19,20),(19,21),(19,25),(19,30);
(20,21),(20,25),(20,30);
(21,25),(21,30);(25,30)共15个基本事件;
满足|x-y|≤2的事件为
(17,19),(19,20),(19,21),(20,21)共4个,
∴所求的概率为P=
.
. |
| x |
| 1 |
| 6 |
样本中大于22的有2人,∴样本的优秀率为
| 2 |
| 6 |
| 1 |
| 3 |
∴12名工人中优秀工人为12×
| 1 |
| 3 |
(2)6人中任取2人,加工的零件个数构成基本事件:
(17,19),(17,20),(17,25),(17,30);
(19,20),(19,21),(19,25),(19,30);
(20,21),(20,25),(20,30);
(21,25),(21,30);(25,30)共15个基本事件;
满足|x-y|≤2的事件为
(17,19),(19,20),(19,21),(20,21)共4个,
∴所求的概率为P=
| 4 |
| 15 |
点评:本题考查了茎叶图的应用问题,解题时应根据茎叶图中的数据,计算平均值与概率问题,是基础题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
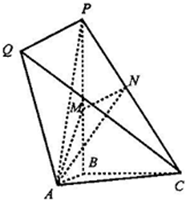 如图所示的几何体中,PB⊥面ABC,PQ∥AB,PQ=PB=1;Rt△ABC中,∠ABC=90°,AB=BC=
如图所示的几何体中,PB⊥面ABC,PQ∥AB,PQ=PB=1;Rt△ABC中,∠ABC=90°,AB=BC=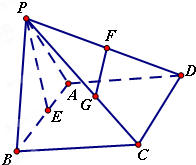 如图,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,△PAB是等边三角形,E、F、G分别是AB、PD、PC的中点.
如图,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,△PAB是等边三角形,E、F、G分别是AB、PD、PC的中点.