题目内容
设函数f(x)的定义域为D,若存在非零实数h,使得对于任意x∈M(M⊆D),有x+h∈D,且f(x+h)≥f(x),则称f(x)为M上的“h阶高调函数”.给出如下结论:
①若函数f(x)在R上单调递增,则存在非零实数h使f(x)为R上的“h阶高调函数”;
②若函数f(x)为R上的“h阶高调函数”,则f(x)在R上单调递增;
③若函数f(x)=x2为区间[-1,+∞)上的“h阶高调函数”,则h≥2;
④若函数f(x)在R上的奇函数,且x≥0时,f(x)=|x-1|-1,则f(x)只能是R上的“4阶高调函数”.
其中正确结论的序号为 .
①若函数f(x)在R上单调递增,则存在非零实数h使f(x)为R上的“h阶高调函数”;
②若函数f(x)为R上的“h阶高调函数”,则f(x)在R上单调递增;
③若函数f(x)=x2为区间[-1,+∞)上的“h阶高调函数”,则h≥2;
④若函数f(x)在R上的奇函数,且x≥0时,f(x)=|x-1|-1,则f(x)只能是R上的“4阶高调函数”.
其中正确结论的序号为
考点:奇偶性与单调性的综合
专题:新定义
分析:根据“h阶高调函数”的定义,逐个命题进行判断即可得到答案.
解答:
 解:对于①,∵函数f(x)在R上单调递增,故存在非零实数h>0满足f(x+h)≥f(x),使f(x)为R上的“h阶高调函数”;①为真命题;
解:对于①,∵函数f(x)在R上单调递增,故存在非零实数h>0满足f(x+h)≥f(x),使f(x)为R上的“h阶高调函数”;①为真命题;
对于②,令函数f(x)=a(常数),则存在非零实数h,满足f(x+h)≥f(x),故f(x)为R上的“h阶高调函数”,但f(x)在R上不单调递增;②为假命题;
对于③,若函数f(x)=x2为区间[-1,+∞)上的“h阶高调函数”,则f(x+h)≥f(x),即(x+h)2≥x2在x∈[-1,+∞)上恒成立,化简得h2+2hx≥0,
∴
,解得h≥2,故③为真命题;
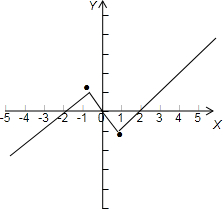
对于④,其图象如图,由图得,存在实数h≥4让其满足定义,则④为假命题.
故答案为:①③.
 解:对于①,∵函数f(x)在R上单调递增,故存在非零实数h>0满足f(x+h)≥f(x),使f(x)为R上的“h阶高调函数”;①为真命题;
解:对于①,∵函数f(x)在R上单调递增,故存在非零实数h>0满足f(x+h)≥f(x),使f(x)为R上的“h阶高调函数”;①为真命题;对于②,令函数f(x)=a(常数),则存在非零实数h,满足f(x+h)≥f(x),故f(x)为R上的“h阶高调函数”,但f(x)在R上不单调递增;②为假命题;
对于③,若函数f(x)=x2为区间[-1,+∞)上的“h阶高调函数”,则f(x+h)≥f(x),即(x+h)2≥x2在x∈[-1,+∞)上恒成立,化简得h2+2hx≥0,
∴
|
对于④,其图象如图,由图得,存在实数h≥4让其满足定义,则④为假命题.
故答案为:①③.
点评:解决本题的关键在于对新定义的理解,只要定义理解透彻,问题就解决了,这也是这一类型题目解决的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
把复数z的共轭复数记作,i为虚数单位.若z=1+i,则(1+z)
等于( )
| z |
| A、3-i | B、3+i |
| C、1+3i | D、3 |
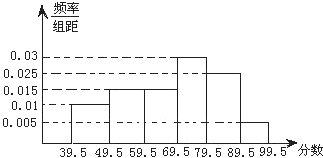 如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图:观察图形,回答下列问题:
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图:观察图形,回答下列问题: