题目内容
设实数x,y满足约束条件
,若目标函数z=(a2+2b2)x+y的最大值为8,则2a+b的最小值为 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用数形结合即可得到结论.
解答:
解: 作出不等式组对应的平面区域如图:由z=(a2+2b2)x+y得y=-(a2+2b2)x+z,
作出不等式组对应的平面区域如图:由z=(a2+2b2)x+y得y=-(a2+2b2)x+z,
由图象可知当y=-(a2+2b2)x+z,经过点A时,目标函数的截距最大,此时z最大,
由
,解得
,即A(1,4),
则a2+2b2+4=8,
即a2+2b2=4,即
+
=1,
设a=2sinθ,b=
cosθ,
则2a+b=4sinθ+
cosθ=3
sin(θ+α),其中α为参数,
则当sin(θ+α)=-1时,2a+b有最小值为-3
,
故答案为:-3
 作出不等式组对应的平面区域如图:由z=(a2+2b2)x+y得y=-(a2+2b2)x+z,
作出不等式组对应的平面区域如图:由z=(a2+2b2)x+y得y=-(a2+2b2)x+z,由图象可知当y=-(a2+2b2)x+z,经过点A时,目标函数的截距最大,此时z最大,
由
|
|
则a2+2b2+4=8,
即a2+2b2=4,即
| a2 |
| 4 |
| b2 |
| 2 |
设a=2sinθ,b=
| 2 |
则2a+b=4sinθ+
| 2 |
| 2 |
则当sin(θ+α)=-1时,2a+b有最小值为-3
| 2 |
故答案为:-3
| 2 |
点评:本题主要考查线性规划的应用,利用数形结合以及三角换元法是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知y=f(x)是偶函数,而y=f(x+1)是奇函数,且对任意0≤x≤1,都有f′(x)≥0,则a=f(
),b=f(
),c=f(
)的大小关系是( )
| 16 |
| 3 |
| 17 |
| 3 |
| 23 |
| 3 |
| A、c<b<a |
| B、c<a<b |
| C、a<c<b |
| D、a<b<c |
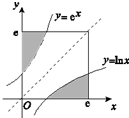 如图,由x=0,x=e,y=0,y=e,y=lnx,y=ex六条曲线共同围成的面积为
如图,由x=0,x=e,y=0,y=e,y=lnx,y=ex六条曲线共同围成的面积为