题目内容
定义在R上的函数f(x)满足f(x+1)=2f(x),且当0≤x≤1时,f(x)=x(1-x);
(1)求当-1≤x≤0时,f(x)的解析式.
(2)求f(x)在[-1,1]上的单调区间和最大值.
(1)求当-1≤x≤0时,f(x)的解析式.
(2)求f(x)在[-1,1]上的单调区间和最大值.
考点:抽象函数及其应用,函数的周期性
专题:函数的性质及应用
分析:(1),令x∈[-1,0],由f(x+1)=2f(x),和f(x)=x(1-x);即可求出函数f(x)的解析式.
(2)利用条件证明函数的单调性,然后利用单调性,求函数的最值即可.
(2)利用条件证明函数的单调性,然后利用单调性,求函数的最值即可.
解答:
解(1)令x∈[-1,0],则x+1∈[0,1]…(1分)
由已知,得f(x)=
f(x+1)=
(x+1)[1-(x+1)]=-
x(x+1)(-1≤x≤0).…(4分)
(2)由(1)知,当0≤x≤1时,f(x)=-(x-
)2+
,…(5分)
则f(x)在[0,
]上单调递增,在[
,1]上单调递减;…(6分)
当-1≤x≤0时,f(x)=-
(x+
)2+
,…(7分)
则f(x)在[-1,-
]上单调递增,在[-
,0]上单调递减;…(8分)
故f(x)在[-1,1]上的单调递增区间为[-1,-
]和[0,
],
单调递减区间为[-
,0]和[
,1];…(9分)
由f(x)在[-1,1]上的单调性知,f(x)在[-1,1]上的最大值为max{f(-
),f(
)};…(11分)
又f(-
)=
,f(
)=
,因此,f(x)在[-1,1]上的最大值为
.…(13分)
由已知,得f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由(1)知,当0≤x≤1时,f(x)=-(x-
| 1 |
| 2 |
| 1 |
| 4 |
则f(x)在[0,
| 1 |
| 2 |
| 1 |
| 2 |
当-1≤x≤0时,f(x)=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
则f(x)在[-1,-
| 1 |
| 2 |
| 1 |
| 2 |
故f(x)在[-1,1]上的单调递增区间为[-1,-
| 1 |
| 2 |
| 1 |
| 2 |
单调递减区间为[-
| 1 |
| 2 |
| 1 |
| 2 |
由f(x)在[-1,1]上的单调性知,f(x)在[-1,1]上的最大值为max{f(-
| 1 |
| 2 |
| 1 |
| 2 |
又f(-
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
点评:本题主要考查抽象函数的应用,利用条件证明函数的单调性是解决本题的关键.

练习册系列答案
相关题目
已知y=f(x)是偶函数,而y=f(x+1)是奇函数,且对任意0≤x≤1,都有f′(x)≥0,则a=f(
),b=f(
),c=f(
)的大小关系是( )
| 16 |
| 3 |
| 17 |
| 3 |
| 23 |
| 3 |
| A、c<b<a |
| B、c<a<b |
| C、a<c<b |
| D、a<b<c |
设a=log
,b=log
,c=(
)0.3 则( )
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| A、c>b>a |
| B、b>a>c |
| C、b>c>a |
| D、a>b>c |
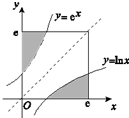 如图,由x=0,x=e,y=0,y=e,y=lnx,y=ex六条曲线共同围成的面积为
如图,由x=0,x=e,y=0,y=e,y=lnx,y=ex六条曲线共同围成的面积为