题目内容
10.设向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a}|=1$,$|{\overrightarrow b}|=2$,$\overrightarrow a,\overrightarrow b$的夹角为$\frac{π}{3}$,则$\overrightarrow a•\overrightarrow b$=( )| A. | 1 | B. | 2 | C. | 3 | D. | 5 |
分析 直接利用数量积公式化简求解即可.
解答 解:向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a}|=1$,$|{\overrightarrow b}|=2$,$\overrightarrow a,\overrightarrow b$的夹角为$\frac{π}{3}$,
则$\overrightarrow a•\overrightarrow b$=$|\overrightarrow{a}||\overrightarrow{b}|cos\frac{π}{3}$=1×$2×\frac{1}{2}$=1.
故选:A.
点评 本题考查平面向量的数量积公式的应用,考查计算能力.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
20.某四面体的三视图如图所示,该四面体的体积为( )


| A. | $\frac{4}{3}$ | B. | 2 | C. | $\frac{8}{3}$ | D. | 4 |
5.甲、乙两人对目标各射击一次,甲命中目标的概率为$\frac{2}{3}$,乙命中目标的概率为$\frac{4}{5}$,若命中目标的人数为X,则D(X)等于( )
| A. | $\frac{85}{225}$ | B. | $\frac{86}{225}$ | C. | $\frac{88}{225}$ | D. | $\frac{89}{225}$ |
19.数列{an}中,${a_{n+1}}+{(-1)^n}{a_n}=2n-1$,则数列{an}前16项和等于( )
| A. | 130 | B. | 132 | C. | 134 | D. | 136 |
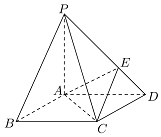 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a,点E在PD上,且PE:ED=2:1;
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a,点E在PD上,且PE:ED=2:1;