题目内容
某旅游景点预计2014年1月份起前x个月的旅游人数的和p(x)(单位:万人)与x的关系近似满足p(x)=
x(x+1)•(39-2x),(x∈N+,x≤12)已知第x月的人均消费额q(x)(单位:元)与x的近似关系是 q(x)=
(1)写出2014年第x月的旅游人数f(x)(单位:万人)与x的函数关系式;
(2)试问2014年哪个月的旅游消费总额最大,最大旅游消费额为多少万元?
| 1 |
| 2 |
|
(1)写出2014年第x月的旅游人数f(x)(单位:万人)与x的函数关系式;
(2)试问2014年哪个月的旅游消费总额最大,最大旅游消费额为多少万元?
考点:分段函数的应用
专题:应用题,函数的性质及应用
分析:(1)先计算x=1时的值,第x月的旅游人数f(x)=P(x)-P(x-1),代入可得结果;
(2)第x月旅游消费总额为g(x)=f(x)•q(x),用分段函数表示,在求每一段的最大值.
(2)第x月旅游消费总额为g(x)=f(x)•q(x),用分段函数表示,在求每一段的最大值.
解答:
解:(1)当x=1时,f(1)=p(1)=37,
当2≤x≤12,且x∈N*时,f(x)=P(x)-P(x-1)=-3x2+40x.
验证:x=1时,37符合f(x))=-3x2+40x
∴f(x))=-3x2+40x(x∈N*,且1≤x≤12))
(2)第x月旅游消费总额为g(x)=f(x)•q(x)=
=
当1≤x≤6,且x∈N+时,g′(x)=18x2-370x+1400,令g′(x)=0,
解得x=5,x=140(舍去)
∴当1≤x<5时,g′(x)>0,当5<x≤6时,g′(x)<0,
∴当x=5时,g(x)max=g(5)=3125(万元)
当7≤x≤12,且x∈N*时,g(x)=-48x+640是减函数,
∴当x=7时,g(x)max=g(7)=304(万元),
综上,2013年第5月份的旅游消费总额最大,最大月旅游消费总额为3125万元.
当2≤x≤12,且x∈N*时,f(x)=P(x)-P(x-1)=-3x2+40x.
验证:x=1时,37符合f(x))=-3x2+40x
∴f(x))=-3x2+40x(x∈N*,且1≤x≤12))
(2)第x月旅游消费总额为g(x)=f(x)•q(x)=
|
|
当1≤x≤6,且x∈N+时,g′(x)=18x2-370x+1400,令g′(x)=0,
解得x=5,x=140(舍去)
∴当1≤x<5时,g′(x)>0,当5<x≤6时,g′(x)<0,
∴当x=5时,g(x)max=g(5)=3125(万元)
当7≤x≤12,且x∈N*时,g(x)=-48x+640是减函数,
∴当x=7时,g(x)max=g(7)=304(万元),
综上,2013年第5月份的旅游消费总额最大,最大月旅游消费总额为3125万元.
点评:本题主要考查实际应用题,读懂题意,列出函数表达式,再应用函数的性质解决实际问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
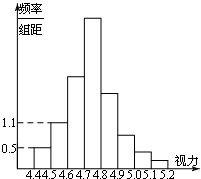 为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道后5组的频数成等比数列,设视力在4.6到4.9之间的学生数为a,最大频率为b,则a,b的值分别为( )
为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道后5组的频数成等比数列,设视力在4.6到4.9之间的学生数为a,最大频率为b,则a,b的值分别为( )| A、77,0.53 |
| B、70,0.32 |
| C、77,5.3 |
| D、70,3.2 |
若ab>0,则下列四个等式:
①lg(ab)=lga+lgb
②lg(
)=lga-lgb
③
lg(
)2=lg(
)
④lg(ab)=
中正确等式的符号是( )
①lg(ab)=lga+lgb
②lg(
| a |
| b |
③
| 1 |
| 2 |
| a |
| b |
| a |
| b |
④lg(ab)=
| 1 |
| logab10 |
| A、①②③④ | B、①② | C、③④ | D、③ |
下列有关命题的说法正确的是( )
| A、命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” |
| B、“x=-1”是“x2-2x-3=0”的必要不充分条件 |
| C、命题“?x∈R使得x2+x-1<0”的否定是“?x∈R,均有x2+x-1>0” |
| D、命题“已知x,y∈R,若x+y≠5,则x≠1或y≠4”为真命题 |