题目内容
9.若存在常数k(k∈N*,k≥2)、d、t(d,t∈R),使得无穷数列{an}满足an+1=$\left\{\begin{array}{l}{{a}_{n}+d,\frac{n}{k}{∉N}^{*}}\\{{ta}_{n},\frac{n}{k}{∈N}^{*}}\end{array}\right.$,则称数列{an}为“段差比数列”,其中常数k、d、t分别叫做段长、段差、段比,设数列{bn}为“段差比数列”.(1)已知{bn}的首项、段长、段差、段比分别为1、2、d、t,若{bn}是等比数列,求d、t的值;
(2)已知{bn}的首项、段长、段差、段比分别为1、3、3、1,其前3n项和为S3n,若不等式${S}_{3n}≤λ{•3}^{n-1}$对n∈N*恒成立,求实数λ的取值范围;
(3)是否存在首项为b,段差为d(d≠0)的“段差比数列”{bn},对任意正整数n都有bn+6=bn.若存在,写出所有满足条件的{bn}的段长k和段比t组成的有序数组(k,t);若不存在,说明理由.
分析 (1){bn}的前4项依次为1,1+d,t(1+d),t(1+d)+d,先求出t,再代入验证,可得结论;
(2)由{bn}的首项、段长、段比、段差,⇒b3n+2-b3n-1=(b3n+1+d)-b3n-1=(qb3n+d)-b3n-1=[q(b3n-1+d)+d]-b3n-1=2d=6,⇒{b3n-1}是等差数列,又b3n-2+b3n-1+b3n=(b3n-1-d)+b3n-1+(b3n-1+d)=3b3n-1,即可求S3n,从而求实数λ的取值范围;
(3)k取2,3,4时存在,有序数组可以是(2,$\frac{b}{b+d}$),(3,$\frac{b}{b+2d}$),(3,-1),(6,$\frac{b}{b+5d}$).
解答 解:(1){bn}的前4项依次为1,1+d,t(1+d),t(1+d)+d,
由前三项成等比数列得(1+d)2=t(1+d),
∵1+≠0,∴t=1+d,
那么第2,3,4项依次为t,t2,t2+t-1,∴t4=t(t2+t-1),∴t=±1.
t=1时,d=0,bn=1,满足题意;
t=-1时,d=-2,bn=(-1)n-1,满足题意;
(2)∵{bn}的首项、段长、段比、段差分别为1、3、1、3,
∴b3n+2-b3n-1=(b3n+1+d)-b3n-1=(qb3n+d)-b3n-1=[q(b3n-1+d)+d]-b3n-1=2d=6,
∴{b3n-1}是以b2=4为首项、6为公差的等差数列,
又∵b3n-2+b3n-1+b3n=(b3n-1-d)+b3n-1+(b3n-1+d)=3b3n-1,
∴S3n=(b1+b2+b3)+(b4+b5+b6)+…+(b3n-2+b3n-1+b3n)=3(b2+b5+…+b3n-1)=3[4n+$\frac{n(n-1)}{2}×6$]=9n2+3n,…(6分)
∵${S}_{3n}≤λ{•3}^{n-1}$,∴$\frac{{S}_{3n}}{{3}^{n-1}}≤λ$,
设cn=$\frac{{S}_{3n}}{{3}^{n-1}}$,则λ≥(cn)max,
又cn+1-cn=$\frac{-2(3{n}^{2}-2n-2)}{{3}^{n-1}}$,
当n=1时,3n2-2n-2<0,c1<c2;当n≥2时,3n2-2n-2>0,cn+1<cn,
∴c1<c2>c3>…,∴(cn)max=c2=14,…(9分)
∴λ≥14,得λ∈[14,+∞).…(10分)
(3)k取2,3,4时存在,有序数组可以是(2,$\frac{b}{b+d}$),(3,$\frac{b}{b+2d}$),(3,-1),(6,$\frac{b}{b+5d}$).
点评 本题考查了等差等比数列的运算及性质,考查了学生的推理和分析能力,属于难题.

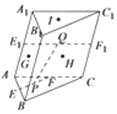 如图,在三棱柱ABC-A1B1C1中,E,F,E1,F1分别为棱AB,AC,AA1,CC1的中点,点G,H分别为四边形ABB1A1,BCC1B1对角线的交点,点I为△A1B1C1的外心,P,Q分别在直线EF,E1F1上运动,则在G,H,I,这三个点中,动直线PQ( )
如图,在三棱柱ABC-A1B1C1中,E,F,E1,F1分别为棱AB,AC,AA1,CC1的中点,点G,H分别为四边形ABB1A1,BCC1B1对角线的交点,点I为△A1B1C1的外心,P,Q分别在直线EF,E1F1上运动,则在G,H,I,这三个点中,动直线PQ( )| A. | 只可能经过点I | B. | 只可能经过点G,H | ||
| C. | 可能经过点G,H,I | D. | 不可能经过点G,H,I |
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 5 | 7.5 | 5 | 2.5 | 5 | 7.5 | 5 | 2.5 | 5 |
| A. | $y=5+\frac{5}{2}sin\frac{π}{12}t,t∈[0,24]$ | B. | $y=5+\frac{5}{2}sin(\frac{π}{12}t+\frac{π}{2}),t∈[0,24]$ | ||
| C. | $y=5+\frac{5}{2}sin\frac{π}{6}t,t∈[0,24]$ | D. | $y=5+\frac{5}{2}sin(\frac{π}{6}t+π),t∈[0,24]$ |
| A. | $\frac{\sqrt{3}+i}{2}$ | B. | -$\sqrt{3}$-i | C. | -$\sqrt{3}$+i | D. | -$\frac{\sqrt{3}+i}{2}$ |
| A. | {3,4} | B. | {1,2,3} | C. | {1,2} | D. | {1,2,3,4} |
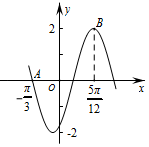 函数f(x)=Asin(ωx+ϕ),($A>0,ω>0,-\frac{π}{2}<ϕ<\frac{π}{2}$)的部分 图象如图所示,则函数f(x)的解析式为f(x)=2sin(2x$-\frac{π}{3}$).
函数f(x)=Asin(ωx+ϕ),($A>0,ω>0,-\frac{π}{2}<ϕ<\frac{π}{2}$)的部分 图象如图所示,则函数f(x)的解析式为f(x)=2sin(2x$-\frac{π}{3}$).