题目内容
20.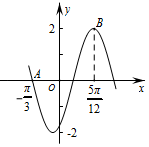 函数f(x)=Asin(ωx+ϕ),($A>0,ω>0,-\frac{π}{2}<ϕ<\frac{π}{2}$)的部分 图象如图所示,则函数f(x)的解析式为f(x)=2sin(2x$-\frac{π}{3}$).
函数f(x)=Asin(ωx+ϕ),($A>0,ω>0,-\frac{π}{2}<ϕ<\frac{π}{2}$)的部分 图象如图所示,则函数f(x)的解析式为f(x)=2sin(2x$-\frac{π}{3}$).
分析 由图象求出函数的周期、最大值A,由周期公式求出ω的值,由函数过的特殊点列出方程,结合条件求出ϕ,可求出函数的解析式.
解答 解:由图可得:A=2,
且$\frac{3}{4}T=\frac{5π}{12}-(-\frac{π}{3})$,解得T=π,
又ω>0,则$\frac{2π}{ω}=π$,解得ω=2,
则函数f(x)=2sin(2x+ϕ),
因为函数图象过点($-\frac{π}{3}$,0),
所以2sin($-\frac{2π}{3}$+ϕ)=0,即$-\frac{2π}{3}$+ϕ=kπ(k∈Z),
解得ϕ=$\frac{2π}{3}$+kπ(k∈Z),
又$-\frac{π}{2}<ϕ<\frac{π}{2}$,则$ϕ=-\frac{π}{3}$,
所以f(x)=2sin(2x$-\frac{π}{3}$),
故答案为:f(x)=2sin(2x$-\frac{π}{3}$).
点评 本题考查由图象求出正弦型函数解析式,三角函数的周期公式,解题的关键是要根据图象分析出函数的最值、周期等,进而求出A,ω和φ值.

练习册系列答案
相关题目
13.下列集合表示正确的是( )
| A. | {2,4} | B. | {2,4,4} | C. | (1,2,3) | D. | {高个子男生} |
12.样本的数据如下:3,4,4,x,5,6,6,7,若该样本平均数为5,则样本方差为( )
| A. | 1.2 | B. | 1.3 | C. | 1.4 | D. | 1.5 |
9.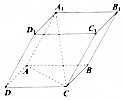 如图,在平行六面体A1C中,AD=AB=AA1=4,∠A1AB=60°,∠BAD=90°,∠A1AD=120°,cos∠A1AC=( )
如图,在平行六面体A1C中,AD=AB=AA1=4,∠A1AB=60°,∠BAD=90°,∠A1AD=120°,cos∠A1AC=( )
 如图,在平行六面体A1C中,AD=AB=AA1=4,∠A1AB=60°,∠BAD=90°,∠A1AD=120°,cos∠A1AC=( )
如图,在平行六面体A1C中,AD=AB=AA1=4,∠A1AB=60°,∠BAD=90°,∠A1AD=120°,cos∠A1AC=( )| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | 0 | D. | $\frac{1}{2}$ |
12.已知函数f(x)=sin(ωx+$\frac{π}{3}$)-$\frac{1}{2}$cos(ωx-$\frac{7π}{6}$)(ω>0)的最小正周期为2π,则f(-$\frac{π}{6}$)=( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{2}$ | C. | $\frac{3\sqrt{3}}{4}$ | D. | $\frac{3\sqrt{3}}{2}$ |
9.已知集合A={x|$\frac{x-2}{x}$≤0},B={0,1,2,3},则A∩B=( )
| A. | {1,2} | B. | {0,1,2} | C. | {1} | D. | {1,2,3} |
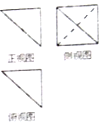 某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积的最大值为2$\sqrt{3}$.
某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积的最大值为2$\sqrt{3}$.