题目内容
17.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,O为坐标原点,P是双曲线在第一象限上的点,直线PO,PF2分别交双曲线C左、右支于另一点M,N,若|PF1|=2|PF2|,且∠MF2N=60°,则双曲线C的离心率为$\sqrt{3}$.分析 由题意,|PF1|=2|PF2|,|PF1|-|PF2|=2a,可得|PF1|=4a,|PF2|=2a,由∠MF2N=60°,可得∠F1PF2=60°,由余弦定理可得4c2=16a2+4a2-2•4a•2a•cos60°,即可求出双曲线C的离心率.
解答  解:由题意,|PF1|=2|PF2|,
解:由题意,|PF1|=2|PF2|,
由双曲线的定义可得,|PF1|-|PF2|=2a,
可得|PF1|=4a,|PF2|=2a,
由四边形PF1MF2为平行四边形,
又∠MF2N=60°,可得∠F1PF2=60°,
在三角形PF1F2中,由余弦定理可得
4c2=16a2+4a2-2•4a•2a•cos60°,
即有4c2=20a2-8a2,即c2=3a2,
可得c=$\sqrt{3}$a,
即e=$\frac{c}{a}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查双曲线C的离心率,注意运用双曲线的定义和三角形的余弦定理,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.已知数列{an}是等差数列,a1=tan$\frac{π}{4}$,a5=13a1,设Sn为数列{(-1)nan}的前n项和,则S2016=( )
| A. | 2016 | B. | -2016 | C. | 3024 | D. | -3024 |
9.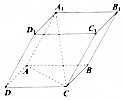 如图,在平行六面体A1C中,AD=AB=AA1=4,∠A1AB=60°,∠BAD=90°,∠A1AD=120°,cos∠A1AC=( )
如图,在平行六面体A1C中,AD=AB=AA1=4,∠A1AB=60°,∠BAD=90°,∠A1AD=120°,cos∠A1AC=( )
 如图,在平行六面体A1C中,AD=AB=AA1=4,∠A1AB=60°,∠BAD=90°,∠A1AD=120°,cos∠A1AC=( )
如图,在平行六面体A1C中,AD=AB=AA1=4,∠A1AB=60°,∠BAD=90°,∠A1AD=120°,cos∠A1AC=( )| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | 0 | D. | $\frac{1}{2}$ |
12.已知函数f(x)=sin(ωx+$\frac{π}{3}$)-$\frac{1}{2}$cos(ωx-$\frac{7π}{6}$)(ω>0)的最小正周期为2π,则f(-$\frac{π}{6}$)=( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{2}$ | C. | $\frac{3\sqrt{3}}{4}$ | D. | $\frac{3\sqrt{3}}{2}$ |
6.为了得到函数$y=sin(2x+\frac{π}{3})$的图象,只需将函数y=sin2x的图象上每一点( )
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向左平移$\frac{π}{6}$个单位长度 | ||
| C. | 向右平移$\frac{π}{3}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
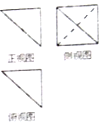 某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积的最大值为2$\sqrt{3}$.
某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积的最大值为2$\sqrt{3}$.