题目内容
16．已知圆x2+y2=4，过点A（4，0）作圆的割线ABC，则弦BC中点的轨迹方程为（ ）| A． | （x-1）2+y2=4 （-1≤x＜$\frac{1}{2}$） | B． | （x-1）2+y2=4 （0≤x＜1） | ||
| C． | （x-2）2+y2=4 （-1≤x＜$\frac{1}{2}$） | D． | （x-2）2+y2=4 （0≤x＜1） |
分析 设弦BC中点（x，y），过A的直线的斜率为k，求得割线ABC的方程．再由弦的中点与圆心连线与割线ABC垂直可得垂线的方程．再根据弦的中点是这两条直线的交点，求出弦的中点的轨迹方程．
解答 
解：设弦BC中点（x，y），过A的直线的斜率为k，
割线ABC的方程：y=k（x-4）；
作圆的割线ABC，所以中点与圆心连线与割线ABC垂直，方程为：x+ky=0；
因为交点就是弦的中点，它在这两条直线上，故弦BC中点的轨迹方程
是：x2+y2-4x=0（已知圆内部分）
即（x-2）2+y2=4（0≤x＜1）
故选：D．
点评 本题考查形式数形结合的数学思想，轨迹方程，直线与圆的方程的应用，中档题．
练习册系列答案
相关题目
1．下列等式一定成立的是（ ）
| A． | a${\;}^{-\frac{1}{2}}$•a${\;}^{\frac{1}{2}}$=0 | B． | a${\;}^{\frac{1}{2}}$÷a${\;}^{\frac{1}{3}}$=a${\;}^{\frac{5}{6}}$ | ||
| C． | （a3）2=a9 | D． | a${\;}^{\frac{1}{2}}$•a${\;}^{\frac{1}{2}}$=a |
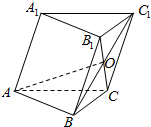已知斜三棱柱ABC-A1B1C1中，∠BAC=$\frac{π}{2}$，∠BAA1=$\frac{2π}{3}$，∠CAA1=$\frac{π}{3}$，AB=AC=1，AA1=2，点O是B1C与BC1的交点．