题目内容
7.已知数列{xn}为等差数列,且x1+x2+x3=5,x18+x19+x20=25,则数列{xn}的前20项的和为100.分析 通过等差中项可知x2=$\frac{5}{3}$,x19=$\frac{25}{3}$,利用数列{xn}的前20项的和为$\frac{20({x}_{2}+{x}_{19})}{2}$,进而计算可得结论.
解答 解:∵数列{xn}为等差数列,
∴2xn+1=xn+xn+2,
又∵x1+x2+x3=5,x18+x19+x20=25,
∴x2=$\frac{5}{3}$,x19=$\frac{25}{3}$,
∴x2+x19=$\frac{5}{3}$+$\frac{25}{3}$=10,
∴数列{xn}的前20项的和为$\frac{20({x}_{2}+{x}_{19})}{2}$=100,
故答案为:100.
点评 本题考查数列的前n项和,考查运算求解能力,注意解题方法的积累,属于基础题.

练习册系列答案
相关题目
14.已知f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2-4x+1,则不等式f(x)>2x2-4的解集为( )
| A. | (-1,2) | B. | (-1,1) | C. | [0,1] | D. | (-1,0] |
18.使不等式|x+1|≤4成立的一个必要不充分条件是( )
| A. | 2≤x≤3 | B. | -6≤x≤3 | C. | -5≤x≤3 | D. | -6≤x≤2 |
12.设集合A={x|-2<x<7 },B={x|x>1,x∈N},则A∩B的元素的个数为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
16.已知圆x2+y2=4,过点A(4,0)作圆的割线ABC,则弦BC中点的轨迹方程为( )
| A. | (x-1)2+y2=4 (-1≤x<$\frac{1}{2}$) | B. | (x-1)2+y2=4 (0≤x<1) | ||
| C. | (x-2)2+y2=4 (-1≤x<$\frac{1}{2}$) | D. | (x-2)2+y2=4 (0≤x<1) |
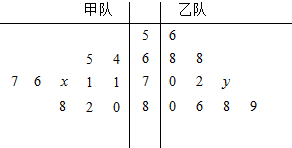 下面的茎叶图记录了甲、乙两代表队各10名同学在一次数学竞赛中的成绩(单位:分),已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.
下面的茎叶图记录了甲、乙两代表队各10名同学在一次数学竞赛中的成绩(单位:分),已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.