题目内容
11.点A(-1,2)关于直线x+y-3=0的对称点B的坐标是(1,4).分析 设出对称点的坐标,利用点的对称的关系建立方程关系进行求解即可.
解答 解:设对称点的坐标为(x,y),
则满足 $\left\{\begin{array}{l}{\frac{y-2}{x+1}•(-1)=-1}\\{\frac{x-1}{2}+\frac{y+2}{2}-3=0}\end{array}\right.$,
即$\left\{\begin{array}{l}{x-y+3=0}\\{x+y-5=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$,即对称点的坐标为(1,4),
故答案为:(1,4).
点评 本题主要考查点的对称的应用,根据对称关系建立方程是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右焦点为M,左顶点为A,以F是为圆心过点A的圆交双曲线的一条渐近线于P,Q两点,若|PQ|不小于双曲线的虚轴长,则该双曲线的离心率的取值范围是( )
| A. | (1,2] | B. | $(1,\sqrt{3}]$ | C. | (1,3] | D. | R |
16.已知圆x2+y2=4,过点A(4,0)作圆的割线ABC,则弦BC中点的轨迹方程为( )
| A. | (x-1)2+y2=4 (-1≤x<$\frac{1}{2}$) | B. | (x-1)2+y2=4 (0≤x<1) | ||
| C. | (x-2)2+y2=4 (-1≤x<$\frac{1}{2}$) | D. | (x-2)2+y2=4 (0≤x<1) |
20.过双曲线$\frac{{x}^{2}}{3}$-y2=1的两焦点作实轴的垂线,分别与渐近线交于A、B、C、D四点,则矩形ABCD的面积为( )
| A. | $\frac{16}{3}$$\sqrt{3}$ | B. | 3 | C. | 8 | D. | 2 |
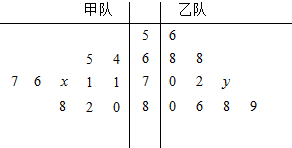 下面的茎叶图记录了甲、乙两代表队各10名同学在一次数学竞赛中的成绩(单位:分),已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.
下面的茎叶图记录了甲、乙两代表队各10名同学在一次数学竞赛中的成绩(单位:分),已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.