题目内容
已知圆A过点P(
,
),且与圆B:(x+2)2+(y-2)2=r2(r>0)关于直线x-y+2=0对称.
(1)求圆A的方程;
(2)若HE、HF是圆A的两条切线,E、F是切点,求
•
的最小值.
(3)过平面上一点Q(x0,y0)向圆A和圆B各引一条切线,切点分别为C、D,设
=2,求证:平面上存在一定点M使得Q到M的距离为定值,并求出该定值.
| 2 |
| 2 |
(1)求圆A的方程;
(2)若HE、HF是圆A的两条切线,E、F是切点,求
| HE |
| HF |
(3)过平面上一点Q(x0,y0)向圆A和圆B各引一条切线,切点分别为C、D,设
| |QD| |
| |QC| |
考点:直线和圆的方程的应用
专题:直线与圆
分析:(1)设出圆心坐标,利用圆与圆B:(x+2)2+(y-2)2=r2(r>0)关于直线x-y+2=0对称,求出圆心坐标,再代入P的坐标,即可得出圆A的方程;
(2)设∠EHF=2θ,|
|=t,利用向量的数量积公式表示出
•
,再利用基本不等式,可求
•
的最小值.
(3)利用
=2,确定Q(x0,y0)的轨迹方程,结合距离公式可得结论.
(2)设∠EHF=2θ,|
| HA |
| HE |
| HF |
| HE |
| HF |
(3)利用
| |QD| |
| |QC| |
解答:
(1)解:设圆A的圆心A(a,b),由题意得:
解得
,
设圆A的方程为x2+y2=r2,将点P(
,
)代入得r=2,
∴圆A的方程为:x2+y2=4;
(2)解:设∠EHF=2θ,|
|=t,
则
•
=|
||
|cos2θ=|
|2cos2θ=(|
|2-4)(1-2sin2θ)=(t2-4)(1-2•
)=t2+
-12≥8
-12
当且仅当t2=
即t=
时取等号,
∴
•
的最小值为8
-12;
(3)由(1)得圆A的方程为:x2+y2=4,圆B:(x+2)2+(y-2)2=4,
由题设得|QD|=2|QC|,即
=2
,
∴(x0+2)2+(y0-2)2-4=4(
+
-4),
化简得:3
+3
-4x0+4y0-20=0,
∴(x0-
)2+(y0+
)2=
,
∴存在定点M(
,-
)使得Q到M的距离为定值
.
|
|
设圆A的方程为x2+y2=r2,将点P(
| 2 |
| 2 |
∴圆A的方程为:x2+y2=4;
(2)解:设∠EHF=2θ,|
| HA |
则
| HE |
| HF |
| HE |
| HF |
| HF |
| HA |
| 4 |
| t2 |
| 32 |
| t2 |
| 2 |
当且仅当t2=
| 32 |
| t2 |
| 4 | 32 |
∴
| HE |
| HF |
| 2 |
(3)由(1)得圆A的方程为:x2+y2=4,圆B:(x+2)2+(y-2)2=4,
由题设得|QD|=2|QC|,即
| QB2-4 |
| QA2-4 |
∴(x0+2)2+(y0-2)2-4=4(
| x | 2 0 |
| y | 2 0 |
化简得:3
| x | 2 0 |
| y | 2 0 |
∴(x0-
| 2 |
| 3 |
| 2 |
| 3 |
| 68 |
| 9 |
∴存在定点M(
| 2 |
| 3 |
| 2 |
| 3 |
2
| ||
| 3 |
点评:本题考查圆的方程,考查向量的数量积公式,考查轨迹方程,考查学分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
已知a>0,x,y满足约束条件
,若z=2x+y的最小值为
,则a=( )
|
| 3 |
| 2 |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
若向量
=(2,0),
=(1,1),则下列结论正确的是( )
| a |
| b |
A、
| ||||||
B、
| ||||||
C、(
| ||||||
D、
|
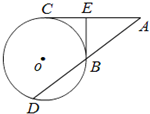 (几何证明选讲选做题)如图,过⊙O外一点A分别作切线AC和割线AD,C为切点,D,B为割线与⊙O的交点,过点B作⊙O的切线交AC于点E.若BE⊥AC,BE=3,AE=4,则DB=
(几何证明选讲选做题)如图,过⊙O外一点A分别作切线AC和割线AD,C为切点,D,B为割线与⊙O的交点,过点B作⊙O的切线交AC于点E.若BE⊥AC,BE=3,AE=4,则DB= 如图,已知椭圆
如图,已知椭圆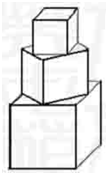 有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边中点,已知最底层正方体的棱长为2,且该塔形的表面积(含C最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边中点,已知最底层正方体的棱长为2,且该塔形的表面积(含C最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是