题目内容
若向量
=(2,0),
=(1,1),则下列结论正确的是( )
| a |
| b |
A、
| ||||||
B、
| ||||||
C、(
| ||||||
D、
|
考点:数量积判断两个平面向量的垂直关系,平行向量与共线向量
专题:平面向量及应用
分析:根据平面向量的数量积的坐标运算公式,模的坐标运算公式以及两向量平行的坐标运算公式,依次求解判断,即可得到正确答案.
解答:
解:向量
=(2,0),
=(1,1),
∵
•
=2×1+0×1=2,故
•
≠1,
∵|
|=
=2,|
|=
=
,
故|
|≠|
|,
∵
-
=(1,-1),
则(
-
)•
=1×1+(-1)×1=0,
故(
-
)⊥
,
∵2×1-0×1=2,
∴
与
不平行,
综上所述,正确的结论是选项C.
故选:C.
| a |
| b |
∵
| a |
| b |
| a |
| b |
∵|
| a |
| 22+02 |
| b |
| 12+12 |
| 2 |
故|
| a |
| b |
∵
| a |
| b |
则(
| a |
| b |
| b |
故(
| a |
| b |
| b |
∵2×1-0×1=2,
∴
| a |
| b |
综上所述,正确的结论是选项C.
故选:C.
点评:本题考查了平面向量数量积的坐标运算,考查了利用数量积判断两个向量的垂直关系,解答的关键是熟记数量积的坐标运算公式.考查了向量模的概念以及模的坐标运算,考查了向量平行的坐标运算.属于基础题.

练习册系列答案
相关题目
圆x2+(y-3)2=1上的动点P到点Q(2,3)的距离的最小值为( )
| A、2 | B、1 | C、3 | D、4 |
 如图,是一个算法程序框图,在集合A={x|-10≤x≤10,x∈R}中随机抽取一个数值做为x输入,则输出的y值落在区间(-5,3)内的概率为( )
如图,是一个算法程序框图,在集合A={x|-10≤x≤10,x∈R}中随机抽取一个数值做为x输入,则输出的y值落在区间(-5,3)内的概率为( )| A、0.4 | B、0.5 |
| C、0.6 | D、0.8 |
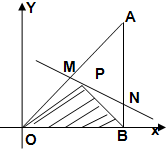 如图所示,将一块直角三角形板ABO置于平面直角坐标系中,已知AB=OB=1,AB⊥OB,点P
如图所示,将一块直角三角形板ABO置于平面直角坐标系中,已知AB=OB=1,AB⊥OB,点P