题目内容
3.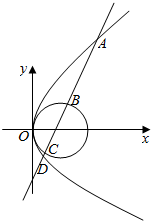 如图,直线y=$\frac{\sqrt{3}}{3}$(x-2)与圆(x-2)2+y2=4及抛物线y2=8x依次交于A,B,C,D四点,则|AB|+|CD|=28.
如图,直线y=$\frac{\sqrt{3}}{3}$(x-2)与圆(x-2)2+y2=4及抛物线y2=8x依次交于A,B,C,D四点,则|AB|+|CD|=28.
分析 由已知圆的方程为(x-2)2+y2=1,抛物线y2=8x的焦点为(2,0),直线y=$\frac{\sqrt{3}}{3}$(x-2)过(2,0)点,则|AB|+|CD|=|AD|-4,直线y=x-2与y2=8x联立可得x2-12x+4=0,由此能够推导出|AB|+|CD|=32-4=28.
解答 解:由已知圆的方程为(x-2)2+y2=1,抛物线y2=8x的焦点为(2,0),直线y=$\frac{\sqrt{3}}{3}$(x-2)过(2,0)点,
则|AB|+|CD|=|AD|-4,
直线y=$\frac{\sqrt{3}}{3}$(x-2)与y2=8x联立可得x2-28x+4=0,
设A(x1,y1),D(x2,y2),则x1+x2=28,
则有|AD|=(x1+x2)+4=32,
故|AB|+|CD|=32-4=28,
故答案为:28
点评 本题考查圆锥曲线和直线的综合运用,等价转化是关键.

练习册系列答案
相关题目
18.命题“?x0∈R,x0+1<0或${x_0}^2-{x_0}>0$”的否定形式是( )
| A. | ?x0∈R,x0+1≥0或${x_0}^2-{x_0}≤0$ | B. | ?x0∈R,x0+1≥0或${x_0}^2-{x_0}≤0$ | ||
| C. | ?x0∈R,x0+1≥0且${x_0}^2-{x_0}≤0$ | D. | ?x0∈R,x0+1≥0且${x_0}^2-{x_0}≤0$ |
15.如图,某地一天中6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(其中A>0,ω>0,-π<φ<π),那么中午12时温度的近似值(精确到1°C)是( )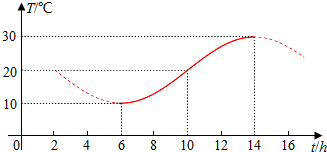

| A. | 25°C | B. | 26°C | C. | 27°C | D. | 28°C |
13.一个锥体的正视图和俯视图如图所示,则该锥体外接球的半径是( )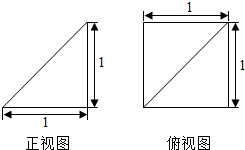

| A. | $\frac{\sqrt{3}}{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2 |