题目内容
13.一个锥体的正视图和俯视图如图所示,则该锥体外接球的半径是( )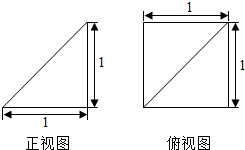
| A. | $\frac{\sqrt{3}}{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2 |
分析 由三视图得该锥体为棱长为1的正方体ABCD-A1B1C1D1中的四棱锥C1-ABCD,由此能求出该锥体外接球的半径.
解答  解:如图,由锥体的三视图得该锥体为四棱锥C1-ABCD,
解:如图,由锥体的三视图得该锥体为四棱锥C1-ABCD,
构造成一个棱长为1的正方体ABCD-A1B1C1D1,
得四棱锥C1-ABCD的外接球即正方体ABCD-A1B1C1D1的外接球,
∴该锥体外接球的半径R=$\frac{1}{2}$AC1=$\frac{\sqrt{3}}{2}$.
故选:A.
点评 本题考查锥体外接球的半径的求法,是中档题,解题时要认真审题,注意构造法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.已知全集U=R,集合A={x|2<x<4},B={x|x2-x-6≤0},则A∩(∁UB)等于( )
| A. | (1,2) | B. | (3,4) | C. | (1,3) | D. | (1,2)∪(3,4) |
8.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,点M在双曲线上,且$\frac{|M{F}_{1}|}{|M{F}_{2}|}$=$\frac{\sqrt{5}-1}{\sqrt{5}+3}$.则双曲线C离心率的最大值为( )
| A. | $\sqrt{5}$+2 | B. | $\frac{\sqrt{5}+2}{2}$ | C. | $\sqrt{5}$-1 | D. | $\frac{\sqrt{5}+1}{2}$ |
18.把函数y=2sin(2x+$\frac{π}{6}$)的图象经过变换,得到y=-2sin2x的图象,这个变换是( )
| A. | 向左平移$\frac{5π}{12}$个单位 | B. | 向右平移$\frac{5π}{12}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位. |
5.求值:cos$\frac{π}{5}$cos$\frac{2π}{5}$=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
3.下列函数中,y的最小值是4的是( )
| A. | y=2x$+\frac{2}{x}$ | B. | y=2x+4•2-x | ||
| C. | y=$\frac{2({x}^{2}+5)}{\sqrt{{x}^{2}+4}}$ | D. | y=$\frac{4}{sinx}+sinx(0<x<4)$ |
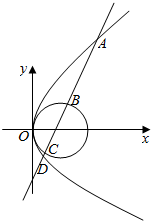 如图,直线y=$\frac{\sqrt{3}}{3}$(x-2)与圆(x-2)2+y2=4及抛物线y2=8x依次交于A,B,C,D四点,则|AB|+|CD|=28.
如图,直线y=$\frac{\sqrt{3}}{3}$(x-2)与圆(x-2)2+y2=4及抛物线y2=8x依次交于A,B,C,D四点,则|AB|+|CD|=28.