题目内容
12.点A(2,-1)到直线x-2y+1=0的距离是$\sqrt{5}$.分析 利用点到直线的距离公式求解.
解答 解:点A(2,-1)到直线x-2y+1=0的距离:
d=$\frac{|2+2+1|}{\sqrt{1+4}}$=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 本题考查点到直线的距离的求法,是基础题,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
相关题目
2.已知函数f(x)=lnx,则f′(2)是( )
| A. | $\frac{1}{2}$ | B. | 0 | C. | 1 | D. | ln2 |
17.设空间两个单位向量$\overrightarrow{OA}$=(m,n,0),$\overrightarrow{OB}$=(0,n,p)与向量$\overrightarrow{OC}$=(1,1,1)的夹角都等于$\frac{π}{4}$,则cos∠AOB=( )
| A. | $\frac{2-\sqrt{3}}{4}$ | B. | $\frac{\sqrt{2}-\sqrt{6}}{4}$ | C. | $\frac{2±\sqrt{3}}{4}$ | D. | $\frac{\sqrt{2}±\sqrt{6}}{4}$ |
4.已知全集U=R,集合A={x|2<x<4},B={x|x2-x-6≤0},则A∩(∁UB)等于( )
| A. | (1,2) | B. | (3,4) | C. | (1,3) | D. | (1,2)∪(3,4) |
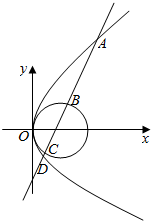 如图,直线y=$\frac{\sqrt{3}}{3}$(x-2)与圆(x-2)2+y2=4及抛物线y2=8x依次交于A,B,C,D四点,则|AB|+|CD|=28.
如图,直线y=$\frac{\sqrt{3}}{3}$(x-2)与圆(x-2)2+y2=4及抛物线y2=8x依次交于A,B,C,D四点,则|AB|+|CD|=28. 如图,在三棱锥K-ABC中,平面KAC⊥平面ABC,KC⊥AC,AC⊥AB,H为KA的中点,KC=AC=AB=2.
如图,在三棱锥K-ABC中,平面KAC⊥平面ABC,KC⊥AC,AC⊥AB,H为KA的中点,KC=AC=AB=2.