题目内容
15.如图,某地一天中6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(其中A>0,ω>0,-π<φ<π),那么中午12时温度的近似值(精确到1°C)是( )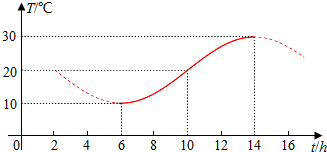
| A. | 25°C | B. | 26°C | C. | 27°C | D. | 28°C |
分析 由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
解答 解:由函数y=Asin(ωx+φ)+b(其中A>0,ω>0,-π<φ<π)的图象,可得b=20°,A=$\frac{30°-10°}{2}$=10°,
$\frac{1}{2}$•$\frac{2π}{ω}$=14-6,求得ω=$\frac{π}{8}$.
再根据五点法作图可得$\frac{π}{8}$•6+φ=$\frac{3π}{2}$,φ=$\frac{3π}{4}$,故 y=10°sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20°.
令x=12,求得y=5$\sqrt{2}$+20≈27°,
故选:C.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,属于基础题.

练习册系列答案
相关题目
6.过抛物线y=x2的焦点F作直线交抛物线于P,Q,若线段PF与QF的长度分别为m,n,则2m+n的最小值为( )
| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{{3+2\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
4.已知全集U=R,集合A={x|2<x<4},B={x|x2-x-6≤0},则A∩(∁UB)等于( )
| A. | (1,2) | B. | (3,4) | C. | (1,3) | D. | (1,2)∪(3,4) |
5.求值:cos$\frac{π}{5}$cos$\frac{2π}{5}$=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
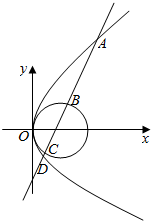 如图,直线y=$\frac{\sqrt{3}}{3}$(x-2)与圆(x-2)2+y2=4及抛物线y2=8x依次交于A,B,C,D四点,则|AB|+|CD|=28.
如图,直线y=$\frac{\sqrt{3}}{3}$(x-2)与圆(x-2)2+y2=4及抛物线y2=8x依次交于A,B,C,D四点,则|AB|+|CD|=28. 如图,在三棱锥K-ABC中,平面KAC⊥平面ABC,KC⊥AC,AC⊥AB,H为KA的中点,KC=AC=AB=2.
如图,在三棱锥K-ABC中,平面KAC⊥平面ABC,KC⊥AC,AC⊥AB,H为KA的中点,KC=AC=AB=2.