题目内容
14.在等差数列{an}中,a1=21,a5=13,试问前几项和最大?最大值多少.分析 利用等差数列通项公式求出公差,由此求出数列前n项和,再利用配方法能求出前几项和最大,最大值多少.
解答 解:∵在等差数列{an}中,a1=21,a5=13,
∴21+4d=13,解得d=-2,
∴${S}_{n}=21n+\frac{n(n-1)}{2}×(-2)$=-n2+22n=-(n-11)2+121.
∴前11项和最大,最大值是121.
点评 本题考查等差数列的前几项和最大,最大值多少的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
4.在空间直角坐标系Oxyz中,点P(1,-2,3)关于x轴的对称点的坐标是( )
| A. | (-1,2,-3) | B. | (1,-2,-3) | C. | (1,2,-3) | D. | (1,-2,-3) |
2.已知函数f(x)=lnx,则f′(2)是( )
| A. | $\frac{1}{2}$ | B. | 0 | C. | 1 | D. | ln2 |
9.已知直线y=kx-1与直线x+2y+3=0垂直,则k的是( )
| A. | 3 | B. | 1 | C. | -1 | D. | 2 |
19.等腰直角三角形ABC(直角边长为2)绕其直角边旋转一周所围成几何体的侧面积为( )
| A. | $4\sqrt{2}π$ | B. | $8\sqrt{2}π$ | C. | 4π | D. | $4\sqrt{2}π+4π$ |
6.过抛物线y=x2的焦点F作直线交抛物线于P,Q,若线段PF与QF的长度分别为m,n,则2m+n的最小值为( )
| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{{3+2\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
4.已知全集U=R,集合A={x|2<x<4},B={x|x2-x-6≤0},则A∩(∁UB)等于( )
| A. | (1,2) | B. | (3,4) | C. | (1,3) | D. | (1,2)∪(3,4) |
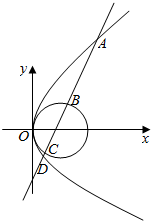 如图,直线y=$\frac{\sqrt{3}}{3}$(x-2)与圆(x-2)2+y2=4及抛物线y2=8x依次交于A,B,C,D四点,则|AB|+|CD|=28.
如图,直线y=$\frac{\sqrt{3}}{3}$(x-2)与圆(x-2)2+y2=4及抛物线y2=8x依次交于A,B,C,D四点,则|AB|+|CD|=28.